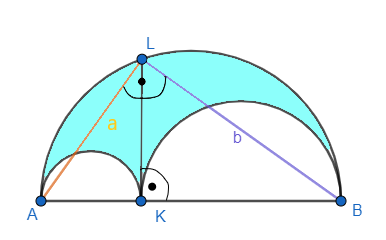
Na średnicy AB wybrano punkt K i narysowano dwa półkola o średnicach AK i KB (jak na rysunku). Udowodnij, że pole zacienionej figury jest równe polu koła, którego średnicą jest odcinek KL, prostopadły do średnicy AB.
![]() – promień okręgu o średnicy |AK|
– promień okręgu o średnicy |AK|
![]() - promień okręgu o średnicy |KB|
- promień okręgu o średnicy |KB|
![]() - promień okręgu o średnicy |AB|
- promień okręgu o średnicy |AB|
![]() - promień okręgu o średnicy |LK|
- promień okręgu o średnicy |LK|
W trójkącie ALB
![]()
![]()
![]()
![]()
Z rysunku
![]()
![]()
![]()

![]()

Przyjmij oznaczenia jak na rysunku powyżej. Trójkąt ALB jest trójkątem prostokątnym, w którym |AB| jest średnicą, a |LK| wysokością, czyli zachodzi równość
![]() . Oblicz pole koła, którego średnicą jest odcinek KL. Za
. Oblicz pole koła, którego średnicą jest odcinek KL. Za
![]() podstaw
podstaw
![]() . Następnie oblicz pole zacieniowanej figury. Od połówki pola okręgu o średnicy AB odejmij połówkę pola okręgu o średnicy AK i połówkę pola okręgu o średnicy KB. Za R podstaw
. Następnie oblicz pole zacieniowanej figury. Od połówki pola okręgu o średnicy AB odejmij połówkę pola okręgu o średnicy AK i połówkę pola okręgu o średnicy KB. Za R podstaw
![]() . Zauważ, że
. Zauważ, że
![]() , co należało udowodnić.
, co należało udowodnić.

Zadanie 1.
154Zadanie 2.
154Zadanie 4.
154Zadanie 5.
154Zadanie 7.
154Zadanie 9.
154Zadanie 14.
155Zadanie 20.
156Zadanie 24.
156Zadanie 26.
156Zadanie 1.
157Zadanie 2.
157Zadanie 3.
157Zadanie 7.
158Zadanie 15.
158Zadanie 17.
162Zadanie 1.
163Zadanie 2.
163Zadanie 3.
163Zadanie 4.
163Zadanie 5.
164Zadanie 6.
164Zadanie 9.
164Zadanie 10.
165Zadanie 11.
165Zadanie 14.
167Zadanie 15.
167Zadanie 16.
167Zadanie 5.
168Zadanie 14.
169Zadanie 17.
169Zadanie 1.
171Zadanie 5.
171Zadanie 8.
171Zadanie 9.
171Zadanie 10.
172Zadanie 11.
172Zadanie 12.
172Zadanie 13.
172Zadanie 18.
173Zadanie 20.
173Zadanie 1.
174Zadanie 3.
174Zadanie 5.
174Zadanie 9.
174Zadanie 14.
175Zadanie 17.
175Zadanie 2.
176Zadanie 4.
176Zadanie 5.
176Zadanie 7.
176Zadanie 18.
177Zadanie 1.
178Zadanie 3.
178Zadanie 18.
179Zadanie 19.
179Zadanie 1.
180Zadanie 8.
180Zadanie 15.
181Zadanie 18.
181Zadanie 22.
182Zadanie 31.
182
