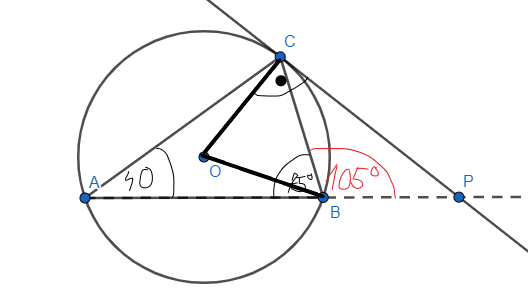
Na trójkącie ABC, gdzie miara kąta ⊾ABC wynosi 75°, a miara kąta ⊾CAB wynosi 40°, opisano okrąg. Styczna do okręgu, poprowadzona przez punkt C, przecina przedłużenie boku AB w punkcie P. Oblicz miary kątów trójkąta BPC.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

Przyjmij oznaczenia jak na rysunku. Kąty ABC i PBC są przyległe, więc kąt PBC ma miarę
![]() . Kąt COB to kąt środkowy, a kąt CAB to kąt wpisany i są one opisane na tym samym łuku CB, więc kąt COB jest dwa razy większy od kąta CAB. Trójkąt COB jest równoramienny, więc kąty przy jego podstawie są równe. Kąt OCP jest kątem prostym, bo prosta, na której się znajduje jest styczną do okręgu. Suma kątów OCB i BCP to
. Kąt COB to kąt środkowy, a kąt CAB to kąt wpisany i są one opisane na tym samym łuku CB, więc kąt COB jest dwa razy większy od kąta CAB. Trójkąt COB jest równoramienny, więc kąty przy jego podstawie są równe. Kąt OCP jest kątem prostym, bo prosta, na której się znajduje jest styczną do okręgu. Suma kątów OCB i BCP to
![]() . Z tego wynika, że miara kąta BCP to
. Z tego wynika, że miara kąta BCP to
![]() . Oblicz miarę kąta BPC korzystając z sumy miar kątów w trójkącie BPC.
. Oblicz miarę kąta BPC korzystając z sumy miar kątów w trójkącie BPC.

Zadanie 1.
154Zadanie 2.
154Zadanie 4.
154Zadanie 5.
154Zadanie 7.
154Zadanie 9.
154Zadanie 14.
155Zadanie 20.
156Zadanie 24.
156Zadanie 26.
156Zadanie 1.
157Zadanie 2.
157Zadanie 3.
157Zadanie 7.
158Zadanie 15.
158Zadanie 17.
162Zadanie 1.
163Zadanie 2.
163Zadanie 3.
163Zadanie 4.
163Zadanie 5.
164Zadanie 6.
164Zadanie 9.
164Zadanie 10.
165Zadanie 11.
165Zadanie 14.
167Zadanie 15.
167Zadanie 16.
167Zadanie 5.
168Zadanie 14.
169Zadanie 17.
169Zadanie 1.
171Zadanie 5.
171Zadanie 8.
171Zadanie 9.
171Zadanie 10.
172Zadanie 11.
172Zadanie 12.
172Zadanie 13.
172Zadanie 18.
173Zadanie 20.
173Zadanie 1.
174Zadanie 3.
174Zadanie 5.
174Zadanie 9.
174Zadanie 14.
175Zadanie 17.
175Zadanie 2.
176Zadanie 4.
176Zadanie 5.
176Zadanie 7.
176Zadanie 18.
177Zadanie 1.
178Zadanie 3.
178Zadanie 18.
179Zadanie 19.
179Zadanie 1.
180Zadanie 8.
180Zadanie 15.
181Zadanie 18.
181Zadanie 22.
182Zadanie 31.
182
