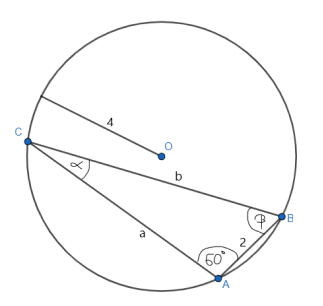
W trójkącie ABC, gdzie długość boku AB wynosi 2, miara kąta BAC wynosi 60°, a promień okręgu opisanego ma wartość 4.Wykaż, że pole trójkąta ABC jest mniejsze od 4√3.
![]()
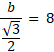
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

Zacznij od obliczenia długości boków b i c z twierdzenia sinusów. Oblicz pole trójkąta ze wzoru
![]() . Pole trójkąta ABC będzie mniejsze od
. Pole trójkąta ABC będzie mniejsze od
![]() gdy wartość
gdy wartość
![]() będzie mniejsza od 1, czyli kąt beta nie może być kątem prostym. Z twierdzenia sinusów oblicz miarę kąta alfa. Nie może ona być równa około
będzie mniejsza od 1, czyli kąt beta nie może być kątem prostym. Z twierdzenia sinusów oblicz miarę kąta alfa. Nie może ona być równa około
![]() , ponieważ suma kątów w trójkącie wynosiłany więcej niż
, ponieważ suma kątów w trójkącie wynosiłany więcej niż
![]() , więc
, więc
![]() , co sprawia, ze
, co sprawia, ze
![]() ,
,
![]() , czyli pole trójkąta ABC będzie mniejsze od
, czyli pole trójkąta ABC będzie mniejsze od
![]() .
.

Zadanie 1.
154Zadanie 2.
154Zadanie 4.
154Zadanie 5.
154Zadanie 7.
154Zadanie 9.
154Zadanie 14.
155Zadanie 20.
156Zadanie 24.
156Zadanie 26.
156Zadanie 1.
157Zadanie 2.
157Zadanie 3.
157Zadanie 7.
158Zadanie 15.
158Zadanie 17.
162Zadanie 1.
163Zadanie 2.
163Zadanie 3.
163Zadanie 4.
163Zadanie 5.
164Zadanie 6.
164Zadanie 9.
164Zadanie 10.
165Zadanie 11.
165Zadanie 14.
167Zadanie 15.
167Zadanie 16.
167Zadanie 5.
168Zadanie 14.
169Zadanie 17.
169Zadanie 1.
171Zadanie 5.
171Zadanie 8.
171Zadanie 9.
171Zadanie 10.
172Zadanie 11.
172Zadanie 12.
172Zadanie 13.
172Zadanie 18.
173Zadanie 20.
173Zadanie 1.
174Zadanie 3.
174Zadanie 5.
174Zadanie 9.
174Zadanie 14.
175Zadanie 17.
175Zadanie 2.
176Zadanie 4.
176Zadanie 5.
176Zadanie 7.
176Zadanie 18.
177Zadanie 1.
178Zadanie 3.
178Zadanie 18.
179Zadanie 19.
179Zadanie 1.
180Zadanie 8.
180Zadanie 15.
181Zadanie 18.
181Zadanie 22.
182Zadanie 31.
182
