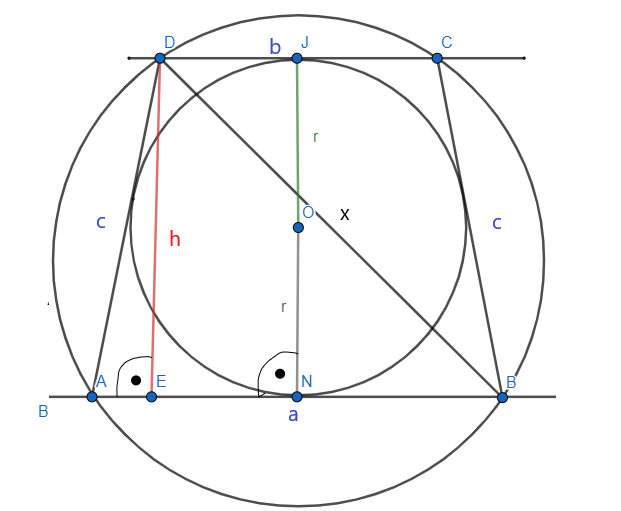
Podany jest trapez, w który można wpisać okrąg i jednocześnie można opisać na nim okrąg. Oblicz promienie oby okręgów, jeśli podano, że podstawy trapezu mają długości a i b (a > b).
![]()
![]()
![]() (trapez równoramienny)
(trapez równoramienny)
![]()
Z tw. Pitagorasa w AED
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Z tw. Pitagorasa w GBD
![]()
![]()
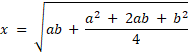
![]()
![]()
![]()
![]()
![]()
![]()
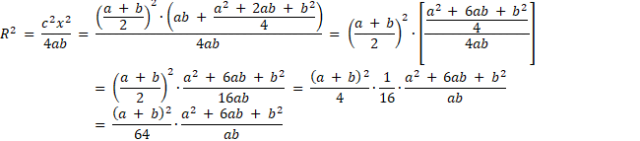
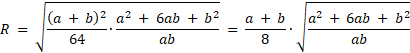

W trapez można wpisać okrąg, jeśli suma długości przeciwległych boków jest identyczna, czyli
![]() . Na trapezie można opisać okrąg, jeżeli suma miar jego przeciwległych kątów jest równa. Jeżeli na trapezie da się opisać okrąg to znaczy, że ten trapez jest równoramienny. Z twierdzenia pitagorasa w trójkącie AED oblicz, że
. Na trapezie można opisać okrąg, jeżeli suma miar jego przeciwległych kątów jest równa. Jeżeli na trapezie da się opisać okrąg to znaczy, że ten trapez jest równoramienny. Z twierdzenia pitagorasa w trójkącie AED oblicz, że
![]() . Zauważ, że h = 2r, więc promień okręgu wpisanego
. Zauważ, że h = 2r, więc promień okręgu wpisanego
![]() . Kolejno oblicz x z twierdzenia Pitagorasa w trójkącie DEB. Oblicz pole trójkąta ABD na dwa sposoby i przyrównaj do siebie wyniki, aby obliczyć promień R, czyli promień okręgu opisanego na trapezie. Dla ułatwienia najpierw policz wartość
. Kolejno oblicz x z twierdzenia Pitagorasa w trójkącie DEB. Oblicz pole trójkąta ABD na dwa sposoby i przyrównaj do siebie wyniki, aby obliczyć promień R, czyli promień okręgu opisanego na trapezie. Dla ułatwienia najpierw policz wartość
![]() , a następnie R.
, a następnie R.

Zadanie 1.
154Zadanie 2.
154Zadanie 4.
154Zadanie 5.
154Zadanie 7.
154Zadanie 9.
154Zadanie 14.
155Zadanie 20.
156Zadanie 24.
156Zadanie 26.
156Zadanie 1.
157Zadanie 2.
157Zadanie 3.
157Zadanie 7.
158Zadanie 15.
158Zadanie 17.
162Zadanie 1.
163Zadanie 2.
163Zadanie 3.
163Zadanie 4.
163Zadanie 5.
164Zadanie 6.
164Zadanie 9.
164Zadanie 10.
165Zadanie 11.
165Zadanie 14.
167Zadanie 15.
167Zadanie 16.
167Zadanie 5.
168Zadanie 14.
169Zadanie 17.
169Zadanie 1.
171Zadanie 5.
171Zadanie 8.
171Zadanie 9.
171Zadanie 10.
172Zadanie 11.
172Zadanie 12.
172Zadanie 13.
172Zadanie 18.
173Zadanie 20.
173Zadanie 1.
174Zadanie 3.
174Zadanie 5.
174Zadanie 9.
174Zadanie 14.
175Zadanie 17.
175Zadanie 2.
176Zadanie 4.
176Zadanie 5.
176Zadanie 7.
176Zadanie 18.
177Zadanie 1.
178Zadanie 3.
178Zadanie 18.
179Zadanie 19.
179Zadanie 1.
180Zadanie 8.
180Zadanie 15.
181Zadanie 18.
181Zadanie 22.
182Zadanie 31.
182
