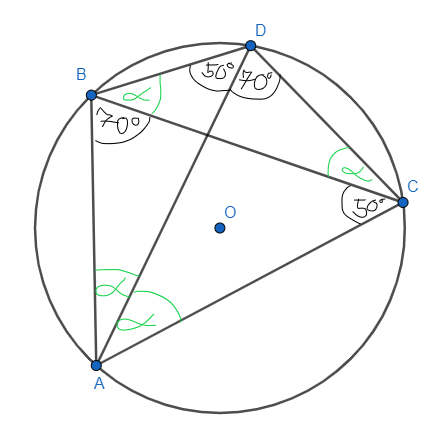
Na okręgu o środku O wybrane zostały punkty A, B i C. Dwusieczna kąta CAB przecina okrąg w punkcie D. Oblicz miary kątów wewnętrznych czworokąta ABCD, przy założeniu, że kąt ABC wynosi 70°, a kąt BCA wynosi 50°.
![]()
![]()
![]()
![]()
![]()
![]()
![]()

Dwusieczna kąta CAB dzieli kąt na dwa kąty każdy o mierze
![]() .
.
Kąty ACB i ADB to kąty wpisane oparte na tym samym łuku AB , więc mają tą samą miarę równą
![]() .
.
Kąty ABC i ADC to kąty wpisane oparte na tym samym łuku AC, więc mają tą samą miarę równą
![]() .
.
Kąty DAC DBC i to kąty wpisane oparte na tym samym łuku DC , więc mają tą samą miarę równą
![]() .
.
Kąty BAD i BCD to kąty wpisane oparte na tym samym łuku BD, więc mają tą samą miarę równą
![]() .
.
Oblicz miarę kąta
![]() z sumy miar kątów w trójkącr ABC i następnie oblicz miary kątów czworokąta ABCD.
z sumy miar kątów w trójkącr ABC i następnie oblicz miary kątów czworokąta ABCD.

Zadanie 1.
154Zadanie 2.
154Zadanie 4.
154Zadanie 5.
154Zadanie 7.
154Zadanie 9.
154Zadanie 14.
155Zadanie 20.
156Zadanie 24.
156Zadanie 26.
156Zadanie 1.
157Zadanie 2.
157Zadanie 3.
157Zadanie 7.
158Zadanie 15.
158Zadanie 17.
162Zadanie 1.
163Zadanie 2.
163Zadanie 3.
163Zadanie 4.
163Zadanie 5.
164Zadanie 6.
164Zadanie 9.
164Zadanie 10.
165Zadanie 11.
165Zadanie 14.
167Zadanie 15.
167Zadanie 16.
167Zadanie 5.
168Zadanie 14.
169Zadanie 17.
169Zadanie 1.
171Zadanie 5.
171Zadanie 8.
171Zadanie 9.
171Zadanie 10.
172Zadanie 11.
172Zadanie 12.
172Zadanie 13.
172Zadanie 18.
173Zadanie 20.
173Zadanie 1.
174Zadanie 3.
174Zadanie 5.
174Zadanie 9.
174Zadanie 14.
175Zadanie 17.
175Zadanie 2.
176Zadanie 4.
176Zadanie 5.
176Zadanie 7.
176Zadanie 18.
177Zadanie 1.
178Zadanie 3.
178Zadanie 18.
179Zadanie 19.
179Zadanie 1.
180Zadanie 8.
180Zadanie 15.
181Zadanie 18.
181Zadanie 22.
182Zadanie 31.
182
