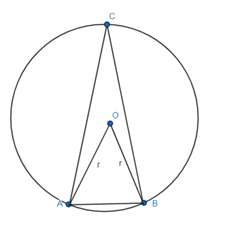
W trójkącie równoramiennym, który jest wpisany w okrąg, jeden z kątów jest oparty na łuku, który jest równy 1/9 długości tego okręgu. Wyznacz miary kątów trójkąta. Rozważ dwa przypadki.
I przypadek
![]()
![]()
![]()
![]()
![]()
Kąty ABC:
![]()
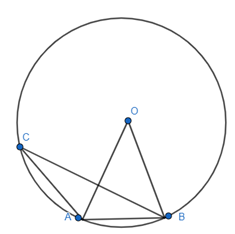
II przypadek
![]()
![]()
![]()
![]()
|AC| = |AB|
![]()
![]()

Rozważ dwa przypadki
I przypadek – odcinek oparty na łuku jest podstawą trójkąta
Zacznij od obliczenia miary kąta AOB. Jest on oparty na łuku równym
![]() długości tego okręgu, czyli jest
długości tego okręgu, czyli jest
![]() kąta
kąta
![]() . Następnie wyznacz miarę kąta ACB. Kąt AOB i kąt ACB to kąty środkowy i wpisany oparte na tym samym łuku, więc
. Następnie wyznacz miarę kąta ACB. Kąt AOB i kąt ACB to kąty środkowy i wpisany oparte na tym samym łuku, więc
![]() . Następnie oblicz miary kątów przy podstawie trójkąta ABC, wiedząc, że są one równe, bo trójkąt jest równoramienny.
. Następnie oblicz miary kątów przy podstawie trójkąta ABC, wiedząc, że są one równe, bo trójkąt jest równoramienny.
II przypadek – odcinek oparty na łuku jest ramieniem trójkąta
Zacznij od obliczenia miary kąta AOB. Jest on oparty na łuku równym
![]() długości tego okręgu, czyli jest
długości tego okręgu, czyli jest
![]() kąta
kąta
![]() . Następnie wyznacz miarę kąta ACB. Kąt AOB i kąt ACB to kąty środkowy i wpisany oparte na tym samym łuku, więc
. Następnie wyznacz miarę kąta ACB. Kąt AOB i kąt ACB to kąty środkowy i wpisany oparte na tym samym łuku, więc
![]() . Miara kąta przy podstawie jest równa
. Miara kąta przy podstawie jest równa
![]() , więc kąt przy wierzchołku będzie miał
, więc kąt przy wierzchołku będzie miał
![]() .
.

Zadanie 1.
154Zadanie 2.
154Zadanie 4.
154Zadanie 5.
154Zadanie 7.
154Zadanie 9.
154Zadanie 14.
155Zadanie 20.
156Zadanie 24.
156Zadanie 26.
156Zadanie 1.
157Zadanie 2.
157Zadanie 3.
157Zadanie 7.
158Zadanie 15.
158Zadanie 17.
162Zadanie 1.
163Zadanie 2.
163Zadanie 3.
163Zadanie 4.
163Zadanie 5.
164Zadanie 6.
164Zadanie 9.
164Zadanie 10.
165Zadanie 11.
165Zadanie 14.
167Zadanie 15.
167Zadanie 16.
167Zadanie 5.
168Zadanie 14.
169Zadanie 17.
169Zadanie 1.
171Zadanie 5.
171Zadanie 8.
171Zadanie 9.
171Zadanie 10.
172Zadanie 11.
172Zadanie 12.
172Zadanie 13.
172Zadanie 18.
173Zadanie 20.
173Zadanie 1.
174Zadanie 3.
174Zadanie 5.
174Zadanie 9.
174Zadanie 14.
175Zadanie 17.
175Zadanie 2.
176Zadanie 4.
176Zadanie 5.
176Zadanie 7.
176Zadanie 18.
177Zadanie 1.
178Zadanie 3.
178Zadanie 18.
179Zadanie 19.
179Zadanie 1.
180Zadanie 8.
180Zadanie 15.
181Zadanie 18.
181Zadanie 22.
182Zadanie 31.
182
