Oblicz obwód trójkąta prostokątnego, który jest opisany na okręgu o promieniu 3, jeśli wiesz, że jego przyprostokątna ma długość 20.
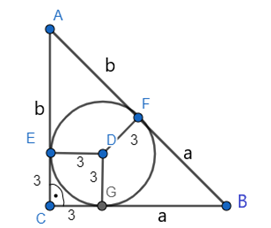
|EA| = |AF| = b
|FB| = |GB| = a
![]()
![]()

Przyjmij oznaczenia jak na rysunku. Czworokąt EDGC jest kwadratem, którego wszystkie boki są równe długości promienia, czyli 3. Skorzystaj z twierdzenia o odcinkach stycznych i stwierdź, że |EA| = |AF| = b i |FB| = |GB| = a. Bok AB ma długość 20 cm, więc a + b = 20 cm. Następnie oblicz obwód trójkąta. Za wyrażenie (a + b) podstaw wartość 20 cm.

Zadanie 1.
154Zadanie 2.
154Zadanie 4.
154Zadanie 5.
154Zadanie 7.
154Zadanie 9.
154Zadanie 14.
155Zadanie 20.
156Zadanie 24.
156Zadanie 26.
156Zadanie 1.
157Zadanie 2.
157Zadanie 3.
157Zadanie 7.
158Zadanie 15.
158Zadanie 17.
162Zadanie 1.
163Zadanie 2.
163Zadanie 3.
163Zadanie 4.
163Zadanie 5.
164Zadanie 6.
164Zadanie 9.
164Zadanie 10.
165Zadanie 11.
165Zadanie 14.
167Zadanie 15.
167Zadanie 16.
167Zadanie 5.
168Zadanie 14.
169Zadanie 17.
169Zadanie 1.
171Zadanie 5.
171Zadanie 8.
171Zadanie 9.
171Zadanie 10.
172Zadanie 11.
172Zadanie 12.
172Zadanie 13.
172Zadanie 18.
173Zadanie 20.
173Zadanie 1.
174Zadanie 3.
174Zadanie 5.
174Zadanie 9.
174Zadanie 14.
175Zadanie 17.
175Zadanie 2.
176Zadanie 4.
176Zadanie 5.
176Zadanie 7.
176Zadanie 18.
177Zadanie 1.
178Zadanie 3.
178Zadanie 18.
179Zadanie 19.
179Zadanie 1.
180Zadanie 8.
180Zadanie 15.
181Zadanie 18.
181Zadanie 22.
182Zadanie 31.
182
