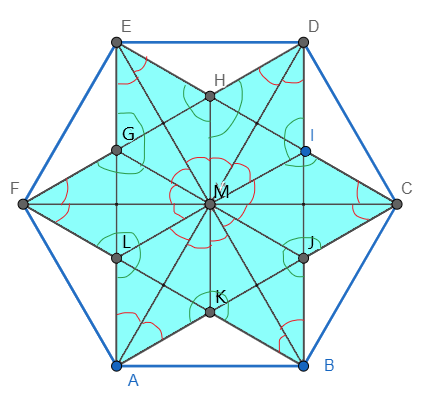
W sześciokącie foremnym narysowano wszystkie krótsze przekątne, tworząc gwiazdę o polu
![]() (zobacz rysunek). Oblicz pole tego sześciokąta.
(zobacz rysunek). Oblicz pole tego sześciokąta.
![]()
![]()
⊾AKB = ⊾BJC = ⊾CID = ⊾DHE = ⊾EGF = ⊾FLA =
![]()
![]()
![]()
Analogicznie w trójkątach
BJC, CID, DHE, EGF, FLA
![]()
![]()
![]()

Zauważ, że pole gwiazdki składa się z 12 trójkątów równoramiennych. Kąty przy podstawie tych trójkątów mają miary
![]() , ponieważ jest to miara równa połowie miary kąta trójkąta równobocznego. Kąty o wartości
, ponieważ jest to miara równa połowie miary kąta trójkąta równobocznego. Kąty o wartości
![]() oznaczone są na rysunku na czerwono. Na zielono oznaczone zostaną kąty o mierze
oznaczone są na rysunku na czerwono. Na zielono oznaczone zostaną kąty o mierze
![]() Zauważ, że miarę każdego z kątów AKB, BJC, CID, DHE, EGF, FLA można obliczyć jako
Zauważ, że miarę każdego z kątów AKB, BJC, CID, DHE, EGF, FLA można obliczyć jako
![]() . Czyli wszystkie te kąty mają miarę
. Czyli wszystkie te kąty mają miarę
![]() Oblicz, że kąty przy podstawach w trójkątach AKB, BJC, CID, DHE, EGF, FLA mają po
Oblicz, że kąty przy podstawach w trójkątach AKB, BJC, CID, DHE, EGF, FLA mają po
![]() . Oznacza to że wszystkie trójkąty o miarach kątów
. Oznacza to że wszystkie trójkąty o miarach kątów
![]() mają identyczne pola. Oblicz pole jednego z takich trójkątów i zauważ, że pole całego cześciokąta składa się z 18 takich trójkątów.
mają identyczne pola. Oblicz pole jednego z takich trójkątów i zauważ, że pole całego cześciokąta składa się z 18 takich trójkątów.

Zadanie 1.
154Zadanie 2.
154Zadanie 4.
154Zadanie 5.
154Zadanie 7.
154Zadanie 9.
154Zadanie 14.
155Zadanie 20.
156Zadanie 24.
156Zadanie 26.
156Zadanie 1.
157Zadanie 2.
157Zadanie 3.
157Zadanie 7.
158Zadanie 15.
158Zadanie 17.
162Zadanie 1.
163Zadanie 2.
163Zadanie 3.
163Zadanie 4.
163Zadanie 5.
164Zadanie 6.
164Zadanie 9.
164Zadanie 10.
165Zadanie 11.
165Zadanie 14.
167Zadanie 15.
167Zadanie 16.
167Zadanie 5.
168Zadanie 14.
169Zadanie 17.
169Zadanie 1.
171Zadanie 5.
171Zadanie 8.
171Zadanie 9.
171Zadanie 10.
172Zadanie 11.
172Zadanie 12.
172Zadanie 13.
172Zadanie 18.
173Zadanie 20.
173Zadanie 1.
174Zadanie 3.
174Zadanie 5.
174Zadanie 9.
174Zadanie 14.
175Zadanie 17.
175Zadanie 2.
176Zadanie 4.
176Zadanie 5.
176Zadanie 7.
176Zadanie 18.
177Zadanie 1.
178Zadanie 3.
178Zadanie 18.
179Zadanie 19.
179Zadanie 1.
180Zadanie 8.
180Zadanie 15.
181Zadanie 18.
181Zadanie 22.
182Zadanie 31.
182
