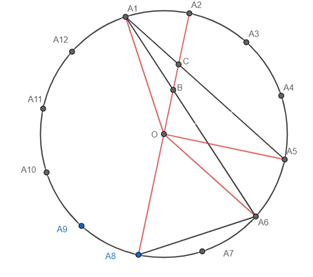
Dwanaście punktów A₁, A₂, A₃, ..., A₁₂ podzieliło okrąg na dwanaście łuków o jednakowej długości. Trzy cięciwy: A₁A₆, A₂A₈, A₅A₁ tworzą wierzchołki pewnego trójkąta. Oblicz miary jego kątów.
![]()
![]()
![]() - kąt środkowy
- kąt środkowy
![]() - kąt środkowy
- kąt środkowy
![]() - trzykrotność kąta środkowego
- trzykrotność kąta środkowego
![]() - dwukrotność kąta środkowego
- dwukrotność kąta środkowego
![]()
![]()
![]() (kąty przyległe)
(kąty przyległe)
![]()
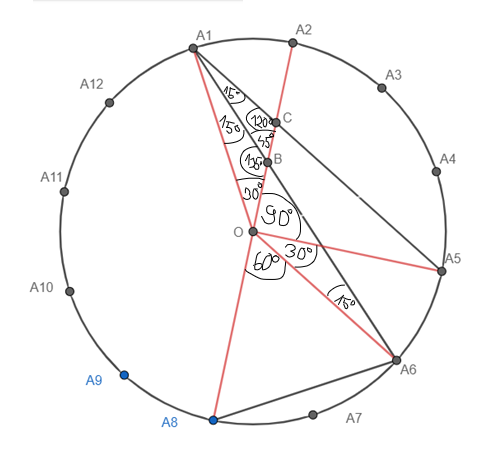
Miary kątów tego trójkąta to
![]()

![]() to kąt środkowy dwunastokąta, czyli ma miarę
to kąt środkowy dwunastokąta, czyli ma miarę
![]() .
.
![]() i kąt środkowy to kąt wpisany i środkowy oparte na tym samym łuku, więc
i kąt środkowy to kąt wpisany i środkowy oparte na tym samym łuku, więc
![]() .
.
Miary kątów
![]() określ przy pomocy wyznaczonej wartości miary kąta środkowego.
określ przy pomocy wyznaczonej wartości miary kąta środkowego.
Trójkąt
![]() jest równoramienny, więc kąty przy jego podstawie są równe.
jest równoramienny, więc kąty przy jego podstawie są równe.
Oblicz miarę kąta
![]() z sumy kątów w trójkącie.
z sumy kątów w trójkącie.
Oblicz miarę kąta
![]() wykorzystując kąty przyległe.
wykorzystując kąty przyległe.
Oblicz miarę kąta
![]() z sumy kątów w trójkącie.
z sumy kątów w trójkącie.

Zadanie 1.
154Zadanie 2.
154Zadanie 4.
154Zadanie 5.
154Zadanie 7.
154Zadanie 9.
154Zadanie 14.
155Zadanie 20.
156Zadanie 24.
156Zadanie 26.
156Zadanie 1.
157Zadanie 2.
157Zadanie 3.
157Zadanie 7.
158Zadanie 15.
158Zadanie 17.
162Zadanie 1.
163Zadanie 2.
163Zadanie 3.
163Zadanie 4.
163Zadanie 5.
164Zadanie 6.
164Zadanie 9.
164Zadanie 10.
165Zadanie 11.
165Zadanie 14.
167Zadanie 15.
167Zadanie 16.
167Zadanie 5.
168Zadanie 14.
169Zadanie 17.
169Zadanie 1.
171Zadanie 5.
171Zadanie 8.
171Zadanie 9.
171Zadanie 10.
172Zadanie 11.
172Zadanie 12.
172Zadanie 13.
172Zadanie 18.
173Zadanie 20.
173Zadanie 1.
174Zadanie 3.
174Zadanie 5.
174Zadanie 9.
174Zadanie 14.
175Zadanie 17.
175Zadanie 2.
176Zadanie 4.
176Zadanie 5.
176Zadanie 7.
176Zadanie 18.
177Zadanie 1.
178Zadanie 3.
178Zadanie 18.
179Zadanie 19.
179Zadanie 1.
180Zadanie 8.
180Zadanie 15.
181Zadanie 18.
181Zadanie 22.
182Zadanie 31.
182
