Dwa okręgi mają jeden punkt wspólny. Przez ten punkt P poprowadzono proste, które są styczne do obu okręgów. Punkty A, B, C, D są punktami styczności tych prostych z okręgami. Udowodnij, że czworokąt ABCD jest trapezem równoramiennym.
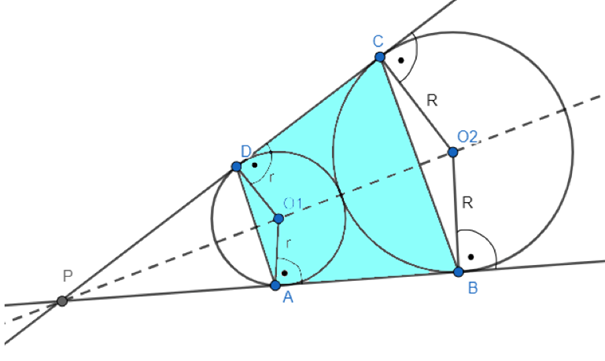
Z cechy kbk
![]()
![]()
![]()
Z cechy kbk
![]()
|BP| = |CP|
![]()
![]()
Z tw. odwrotnego do twierdzenia Talesa
AD || BC
![]()

Zacznij od skorzystania z przystawania trójkątów
![]() oraz
oraz
![]() , aby dojść do równości
, aby dojść do równości
![]() i
i
![]() . Z tego wynika, że
. Z tego wynika, że
![]() . Skorzystaj z twierdzenia odwrotnego do twierdzenia Talesa i wskaż, ze prosta AD jest równoległa do prostej BC. Następnie zauważ, że |AB| = |DC|. Pokazaliśmy, że |AB| = |DC| i AD || BC, czyli czworokąt ABCD jest trapezem równoramiennym.
. Skorzystaj z twierdzenia odwrotnego do twierdzenia Talesa i wskaż, ze prosta AD jest równoległa do prostej BC. Następnie zauważ, że |AB| = |DC|. Pokazaliśmy, że |AB| = |DC| i AD || BC, czyli czworokąt ABCD jest trapezem równoramiennym.

Zadanie 1.
154Zadanie 2.
154Zadanie 4.
154Zadanie 5.
154Zadanie 7.
154Zadanie 9.
154Zadanie 14.
155Zadanie 20.
156Zadanie 24.
156Zadanie 26.
156Zadanie 1.
157Zadanie 2.
157Zadanie 3.
157Zadanie 7.
158Zadanie 15.
158Zadanie 17.
162Zadanie 1.
163Zadanie 2.
163Zadanie 3.
163Zadanie 4.
163Zadanie 5.
164Zadanie 6.
164Zadanie 9.
164Zadanie 10.
165Zadanie 11.
165Zadanie 14.
167Zadanie 15.
167Zadanie 16.
167Zadanie 5.
168Zadanie 14.
169Zadanie 17.
169Zadanie 1.
171Zadanie 5.
171Zadanie 8.
171Zadanie 9.
171Zadanie 10.
172Zadanie 11.
172Zadanie 12.
172Zadanie 13.
172Zadanie 18.
173Zadanie 20.
173Zadanie 1.
174Zadanie 3.
174Zadanie 5.
174Zadanie 9.
174Zadanie 14.
175Zadanie 17.
175Zadanie 2.
176Zadanie 4.
176Zadanie 5.
176Zadanie 7.
176Zadanie 18.
177Zadanie 1.
178Zadanie 3.
178Zadanie 18.
179Zadanie 19.
179Zadanie 1.
180Zadanie 8.
180Zadanie 15.
181Zadanie 18.
181Zadanie 22.
182Zadanie 31.
182
