O pewnym walcu wiadomo, że jego pole powierzchni bocznej wynosi 12π cm2. Sprawdź, czy walec z podpunktu a) ma również najmniejszą objętość.
Skorzystaj z danych z poprzedniego podpunktu:
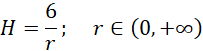
Wyznacz funkcję opisującą objętość walca względem długości promienia podstawy:
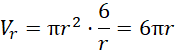
Wyznacz miejsce zerowe pochodnej tej funkcji:
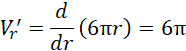
Pochodna to funkcja stała o wartości większej od zera – objętość w zależności od promienia podstawy jest wartością monotonicznie rosnącą. Pochodna nie ma żadnych miejsc zerowych w danym przedziale – nie ma więc ekstremów.
Odp. Walec z podpunktu a) nie osiąga najmniejszej objętości, ponieważ pochodna funkcji objętości nie zeruje się na danym przedziale (jest funkcją stałą).

Wykorzystaj długości wyznaczone w podpunkcie a). Podstaw długości do wzoru na objętość walca. Miejsca zerowe pochodnej wyznaczonej funkcji wskazują na prawdopodobne ekstrema lokalne. Potwierdź, że w dziedzinie funkcji brak zer pochodnej.

Zadanie 6.1.
144Zadanie 6.2.
144Zadanie 6.4.
144Zadanie 6.11.
145Zadanie 6.19.
146Zadanie 6.20.
146Zadanie 6.31.
147Zadanie 6.32.
147Zadanie 6.33.
147Zadanie 6.34.
147Zadanie 6.36.
148Zadanie 6.37.
148Zadanie 6.40.
148Zadanie 6.41.
148Zadanie 6.42.
148Zadanie 6.46.
149Zadanie 6.56.
150Zadanie 6.57.
150Zadanie 6.58.
150Zadanie 6.62.
150Zadanie 6.63.
150Zadanie 6.64.
150Zadanie 6.74.
152Zadanie 6.88.
153Zadanie 6.89.
153Zadanie 6.91.
153Zadanie 6.100.
155Zadanie 6.101.
155Zadanie 6.102.
156Zadanie 6.103.
156Zadanie 6.105.
156Zadanie 6.107.
156Zadanie 6.110.
157Zadanie 16.
159
