O pewnym stożku wiadomo, że miara kąta między ramionami jego przekroju osiowego jest równa 90°, natomiast długość ramion wynosi
![]() . Oblicz objętość kuli wpisanej w stożek o takim przekroju.
. Oblicz objętość kuli wpisanej w stożek o takim przekroju.
Naszkicuj sytuację przedstawioną w treści zadania:
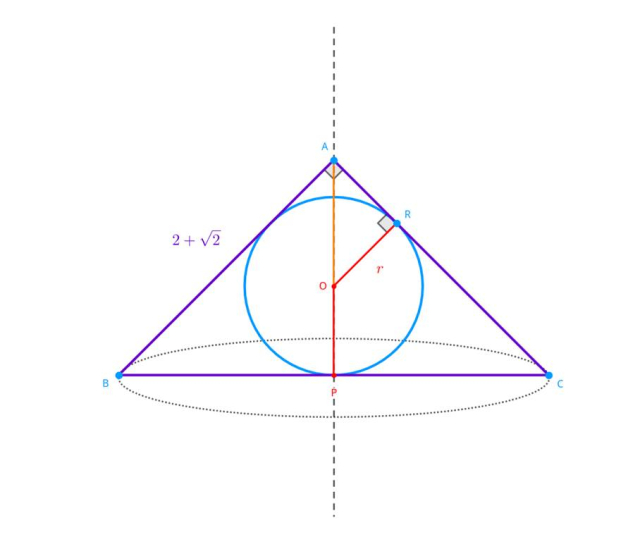
Trójkąt ABC jest trójkątem prostokątnym równoramiennym, zatem:
![]()
Trójkąt ORA również jest trójkątem prostokątnym równoramiennym:
![]()
Długość odcinka AP wyrażona w długościach promienia okręgu wpisanego wynosi:
![]()
Mamy więc:
![]()
![]()
![]()
![]()
![]()
Objętość kuli wynosi:
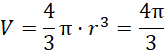
Odp. Objętość kuli wpisanej w ten stożek wynosi
![]() .
.

Rozpoznaj w przekroju osiowym stożka trójkąt prostokątny równoramienny. Wyraź długość ramienia przekroju za pomocą długości promienia okręgu wpisanego. Oblicz długość promienia a następnie objętość kuli.

Zadanie 6.1.
144Zadanie 6.2.
144Zadanie 6.4.
144Zadanie 6.11.
145Zadanie 6.19.
146Zadanie 6.20.
146Zadanie 6.31.
147Zadanie 6.32.
147Zadanie 6.33.
147Zadanie 6.34.
147Zadanie 6.36.
148Zadanie 6.37.
148Zadanie 6.40.
148Zadanie 6.41.
148Zadanie 6.42.
148Zadanie 6.46.
149Zadanie 6.56.
150Zadanie 6.57.
150Zadanie 6.58.
150Zadanie 6.62.
150Zadanie 6.63.
150Zadanie 6.64.
150Zadanie 6.74.
152Zadanie 6.88.
153Zadanie 6.89.
153Zadanie 6.91.
153Zadanie 6.100.
155Zadanie 6.101.
155Zadanie 6.102.
156Zadanie 6.103.
156Zadanie 6.105.
156Zadanie 6.107.
156Zadanie 6.110.
157Zadanie 16.
159
