Dana jest pewna kula z dwoma równoległymi przekrojami o polach kolejno 49π i 4π. Wyznacz pole powierzchni całkowitej całej kuli wiedząc, że przekroje te oddalone są od siebie o 9 jednostek.
Oznaczenia:
R – promień całej kuli
r1 – promień przekroju o polu 49π
r2 – promień przekroju o polu 4π
![]()
![]()
![]()
![]()
![]()
![]()
Promień większego przekroju jest mniejszy od odległości między tymi przekrojami. Pozwala to stwierdzić, że środek kuli znajduje się pomiędzy tymi przekrojami.
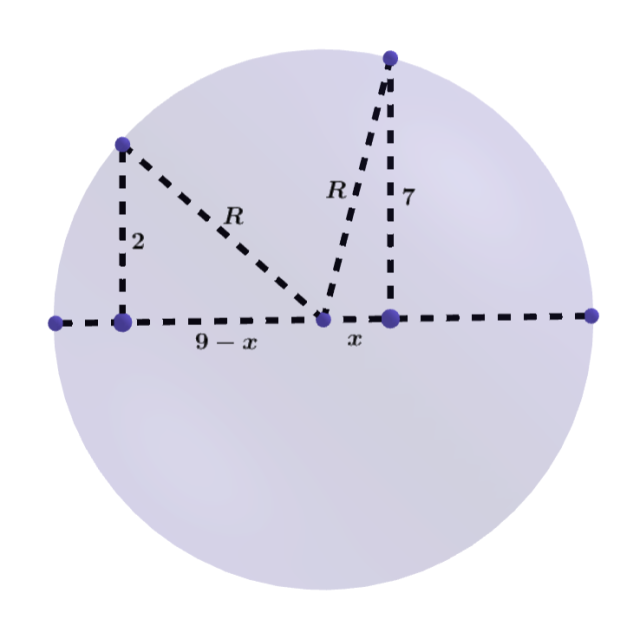
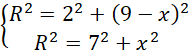
![]()
![]()
![]()
Wstaw tę wartość do jednego z powyższych równań:
![]()
![]()
![]()
Mając promień kuli oblicz jej pole powierzchni:
![]()

Wprowadź odpowiednie oznaczenia i oblicz promienie poszczególnych przekrojów.
Zwróć uwagę, że środek kuli leży pomiędzy tymi przekrojami.
Stwórz rysunek pomocniczy i zaznacz na nim odpowiednie trójkąty prostokątne. Korzystając z twierdzenia Pitagorasa ułóż układ równań i wyznacz z niego promień kuli.
Na koniec wstaw go do wzoru na pole powierzchni:
![]()

Zadanie 6.1.
144Zadanie 6.2.
144Zadanie 6.4.
144Zadanie 6.11.
145Zadanie 6.19.
146Zadanie 6.20.
146Zadanie 6.31.
147Zadanie 6.32.
147Zadanie 6.33.
147Zadanie 6.34.
147Zadanie 6.36.
148Zadanie 6.37.
148Zadanie 6.40.
148Zadanie 6.41.
148Zadanie 6.42.
148Zadanie 6.46.
149Zadanie 6.56.
150Zadanie 6.57.
150Zadanie 6.58.
150Zadanie 6.62.
150Zadanie 6.63.
150Zadanie 6.64.
150Zadanie 6.74.
152Zadanie 6.88.
153Zadanie 6.89.
153Zadanie 6.91.
153Zadanie 6.100.
155Zadanie 6.101.
155Zadanie 6.102.
156Zadanie 6.103.
156Zadanie 6.105.
156Zadanie 6.107.
156Zadanie 6.110.
157Zadanie 16.
159
