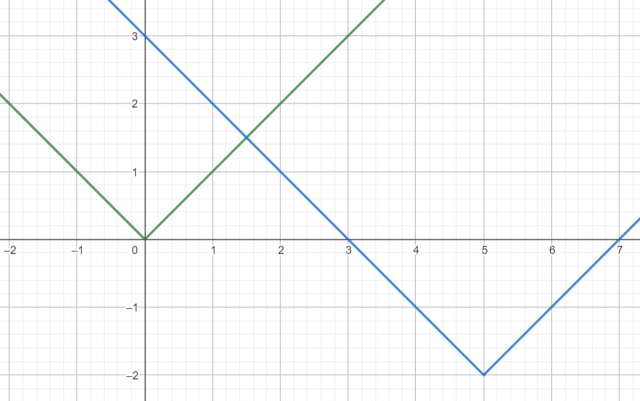
W tym zadaniu musisz naszkicować wykres funkcji f przesunięty o dany wektor [5, -2]. Następnie podaj wzór, który opisuje otrzymany wykres oraz najmniejszą wartość, jaką przyjmuje znaleziona funkcja.
![]()
![]()
najmniejsza wartość funkcji: -2

Przesunięcie wykresu funkcji o wektor [a, b] potraktuj jak złożenie dwóch osobnych przesunięć, jednego o wektor [a, 0] i drugiego o wektor [0, b]. Aby wykres funkcji g(x) był przesunięciem wykresu funkcji f(x) o wektor [a, 0] musi zachodzić równość g(x) = f(x – a). Aby wykres funkcji h był przesunięty względem wykresu funkcji f o wektor [0, b] musi zachodzić równość: h(x) = f(x) + b. Zapisując te zależności wyznacz wzór funkcji g.

Zadanie 1
10Zadanie 2
10Zadanie 3
10Zadanie 4
10Zadanie 5
10Ćwiczenie 2
12Zadanie 1
18Zadanie 4
18Zadanie 5
18Zadanie 6
18Zadanie 7
19Zadanie 8
19Zadanie 9
19Zadanie 10
19Zadanie 11
19Zadanie 12
19Zadanie 13
19Zadanie 14
19Zadanie 15
20Ćwiczenie 4
23Zadanie 1
23Zadanie 2
24Zadanie 3
24Zadanie 4
24Zadanie 10
24Zadanie 11
24Zadanie 1
27Zadanie 3
27Zadanie 4
27Zadanie 5
27Zadanie 6
27Zadanie 7
27Zadanie 8
27Zadanie 1
31Zadanie 2
31Zadanie 3
31Zadanie 4
31Zadanie 5
31Zadanie 6
31Zadanie 7
31Zadanie 1
34Zadanie 2
34Zadanie 6
34Zadanie 1
38Zadanie 2
38Zadanie 3
38Zadanie 6
38Ćwiczenie 1
40Ćwiczenie 3
40Ćwiczenie 5
42Zadanie 2
44Zadanie 3
44Zadanie 4
44Zadanie 5
44Zadanie 6
44Zadanie 7
44Zadanie 1
47Zadanie 2
48Zadanie 3
48Zadanie 4
48Zadanie 5
48Zadanie 6
48Zadanie 7
48Zadanie 8
48Zadanie 9
48Ćwiczenie 1
49Zadanie 1
51Zadanie 2
51Zadanie 16
53Zadanie 17
54Zadanie 18
54Zadanie 19
54Zadanie 20
54Zadanie 21
54Zadanie 22
54Zadanie 23
54Zadanie 24
54Zadanie 26
55Zadanie 27
55Zadanie 28
55Zadanie 29
55Zadanie 30
55Zadanie 31
55Zadanie 32
55
