W tym zadaniu musisz obliczyć pole powierzchni sześcianu, pola widocznych ścian klocków i wyznaczyć, które klocki są pomalowane na biało, a które na czarno.
10 · 10 = 100 cm2
P = 6 · 100 = 600 cm2
20% = 0,2
0,2 · 600 = 120 cm2
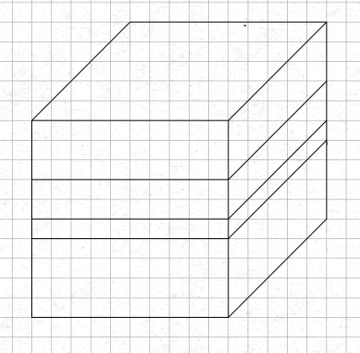
2 klocki o najmniejszej wysokości muszą znajdować się w środku, ponieważ sama górna ściana zajmuje 100 cm2, więc wtedy widoczna biała ściana u góry byłaby prawie tak duża, jak suma pól, której szukamy.
10 · 1 = 10 cm2
10 · 2 = 20 cm2
P = 4 · 10 + 4 · 20 = 40 + 80 = 120 cm2
Klocki o wysokości 1 cm i 2 cm są pomalowane na biało, a klocki o wysokości 3 cm i 4 cm na czarno.

Oblicz pole powierzchni całkowitej sześcianu. Następnie oblicz, ile to jest 20% (czyli 0,2) pola powierzchni sześcianu (czyli 0,2) i narysuj sobie rysunek poglądowy, w jaki sposób mogłyby być klocki ułożone. Górna ściana ma powierzchnie 100 cm2, więc gdyby była biała, równałaby się prawie wynikowi, którego szukamy, dlatego najmniejsze klocki muszą znajdować się w środku. Oblicz pole powierzchni widocznych ścian najmniejszych klocków (czyli suma pól ścian bocznych bez podstaw) i widzisz, że równa się ono 20%, które wcześniej obliczyliśmy.

Zadanie 2
116Zadanie 3
116Zadanie 5
116Zadanie 6
116Zadanie 8
117Zadanie 11
117Zadanie 14
118Zadanie 15
118Zadanie 1
119Zadanie 2
119Zadanie 5
119Zadanie 6
119Zadanie 11
120Zadanie 12
120Zadanie 13
120Zadanie 14
120Zadanie 15
120Zadanie 19
120Zadanie 20
121Zadanie 1
122Zadanie 2
122Zadanie 4
122Zadanie 5
122Zadanie 7
123Zadanie 12
123Zadanie 14
124Zadanie 15
124Zadanie 1
125Zadanie 6
126Zadanie 8
126Zadanie 10
126Zadanie 17
127Zadanie 1
128Zadanie 2
128Zadanie 5
128Zadanie 7
128Zadanie 11
129
