W tym zadaniu oblicz pole powierzchni całkowitej ostrosłupa.
25

W pierwszej kolejności oblicz pozostałe długości krawędzi podstawy korzystając z twierdzenia Pitagorasa.
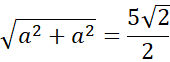
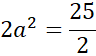
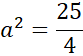
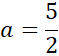 Następnie oblicz pole podstawy.
Następnie oblicz pole podstawy.
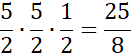 W kolejnym kroku oblicz pola tych ścian bocznych, których krawędź jest prostopadła do podstawy.
W kolejnym kroku oblicz pola tych ścian bocznych, których krawędź jest prostopadła do podstawy.
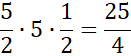 Następnie korzystając z twierdzenia Pitagorasa, oblicz długości pozostałych krawędzi bocznych. Zauważ, że są one sobie równe z własności przystawania trójkątów.
Następnie korzystając z twierdzenia Pitagorasa, oblicz długości pozostałych krawędzi bocznych. Zauważ, że są one sobie równe z własności przystawania trójkątów.
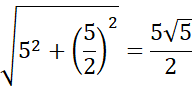 W kolejnym kroku oblicz wysokość ściany bocznej, która nie jest trójkątem prostokątnym. Również skorzystaj z twierdzenia Pitagorasa.
W kolejnym kroku oblicz wysokość ściany bocznej, która nie jest trójkątem prostokątnym. Również skorzystaj z twierdzenia Pitagorasa.
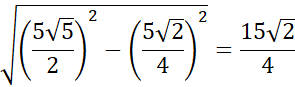 Następnie oblicz pole tego trójkąta.
Następnie oblicz pole tego trójkąta.
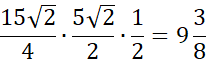 Na koniec dodaj do siebie pola wszystkich ścian.
Na koniec dodaj do siebie pola wszystkich ścian.
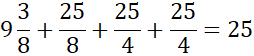

Zadanie 1.
131Zadanie 5.
131Zadanie 6.
131Zadanie 7.
131Zadanie 8.
132Zadanie 9.
132Zadanie 10.
132Zadanie 16.
133Zadanie 18.*
133Zadanie 2.
134Zadanie 4.
134Zadanie 5.
134Zadanie 6.
135Zadanie 7.
135Zadanie 8.
135Zadanie 9.
135Zadanie 10.
135Zadanie 11.
135Zadanie 12.
136Zadanie 14.
136Zadanie 17.*
136Zadanie 2.
138Zadanie 3.
138Zadanie 5.
138Zadanie 6.
138Zadanie 8.
139Zadanie 9.
139Zadanie 10.
139Zadanie 11.
139Zadanie 12.
139Zadanie 13.*
140Zadanie 15.*
140Zadanie 16.
140Zadanie 17.
140Zadanie 18.
141Zadanie 1.
141Zadanie 3.
141Zadanie 4.
142Zadanie 6.
142Zadanie 7.
143Zadanie 8.
143Zadanie 10.
143Zadanie 12.
143Zadanie 19.
144Zadanie 21.*
144Zadanie 1.
146Zadanie 2.
146Zadanie 3.
142Zadanie 5.
147Zadanie 7.
147Zadanie 8.
147Zadanie 9.
147Zadanie 10.
148Zadanie 11.
148Zadanie 12.
148Zadanie 13.
148Zadanie 17.
149Zadanie 18.
149Zadanie 19.
149Zadanie 20.*
149Zadanie 1.
151Zadanie 3.
152Zadanie 4.
152Zadanie 5.
152Zadanie 6.
152Zadanie 8.
153Zadanie 12.
153Zadanie 14.
154Zadanie 15.*
154Zadanie 10.
156Zadanie 20.
158Zadanie 22.
159Zadanie 23.
159
