Prosto do matury. Klasa 3. Zakres podstawowy. Podręcznik - rozwiązania i odpowiedzi

Podręcznik, Wydawnictwo: Nowa Era

Zadanie 5.14 - strona 30

W tym zadaniu masz udowodnić, że dla każdego kąta $\text{[math]}$ podana równość jest tożsamością.
$\text{[math]}$

$\text{[math]}$

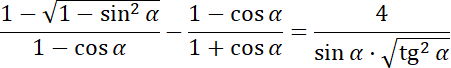
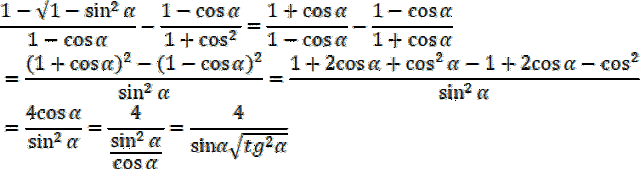
W pierwszym kroku wyznaczamy długość przeciwprostokątnej za pomocą twierdzenia Pitagorasa. Następnie obliczamy obwód trójkąta. Kolejnym krokiem jest obliczenie pola powierzchni trójkąta. Ostatecznie, znajdujemy promień okręgu wpisanego w trójkąt, dzieląc pole naszego trójkąta przez pół obwodu tego trójkąta.

Zadanie 25., strona 120, MATeMAtyka. Klasa 3. Zbiór zadań. Zakres podstawowy – rozwiązania i odpowiedzi

Zadanie sprawdzające 1, strona 92, Matematyka. Klasa 5. Podręcznik – rozwiązania i odpowiedzi

Zadanie 12, strona 46, MATeMAtyka 2. Zakres podstawowy. Podręcznik - rozwiązania i odpowiedzi

Zadanie sprawdzające 1., strona 11, Matematyka wokół nas. Klasa 5. Podręcznik - rozwiązania i odpowiedzi

Zadanie 4., strona 405, Prosto do matury. Matematyka. Klasa 1. Zakres podstawowy. Podręcznik - rozwiązania i odpowiedzi

Ćwiczenie 5., strona 99, Matematyka z plusem. Klasa 5. Zeszyt ćwiczeń. Wersja C - rozwiązania i odpowiedzi

Zadanie 2, strona 31, Matematyka. Klasa 7. Zeszyt ćwiczeń - rozwiązania i odpowiedzi

Ćwiczenie 4, strona 48, Matematyka z Plusem. Klasa 4. Zeszyt ćwiczeń. Wersja B. Część 2/2 - rozwiązania i odpowiedzi

Zadanie 5., strona 193, Matematyka. Klasa 7. Zbiór zadań – rozwiązania i odpowiedzi

Zadanie 5., strona 28, Matematyka wokół nas. Klasa 7. Podręcznik - rozwiązania i odpowiedzi

14

14

14

14

Zadanie 1.5

14

14

14

14

14

14

Zadanie 1.7

14

14

14

14

15

15

15

15

Zadanie 1.12

15

15

15

15

15

15

15

15

15

14

15

15

15

Zadanie Prosto do matury – 1.1

30

Zadanie Prosto do matury – 1.2

30

Zadanie Prosto do matury – 1.3

30

Zadanie Prosto do matury – 1.4

30

Zadanie Prosto do matury – 1.5

30

21

21

21

Zadanie 2.4

21

21

21

21

21

21

21

21

Zadanie 2.8

21

21

21

21

21

Zadanie 2.9

21

21

21

21

21

23

23

23

23

23

23

23

23

23

23

23

23

23

23

23

Zadanie Prosto do matury – 2.1

30

Zadanie Prosto do matury – 2.2

30

Zadanie Prosto do matury – 2.3

30

Zadanie Prosto do matury – 2.5

30

30

30

30

30

30

30

30

Zadanie 3.9

31

31

31

31

31

31

31

31

31

31

31

31

31

31

Zadanie Prosto do matury - 1

30

Zadanie Prosto do matury - 2

30

Zadanie Prosto do matury - 3

30

Zadanie Prosto do matury - 4

30

Zadanie Prosto do matury - 5

30

44

44

44

Zadanie 4.4

44

44

44

44

44

44

44

45

Zadanie 4.7

45

45

45

45

Zadanie 4.8

45

45

45

45

45

45

45

Zadanie 4.9

45

45

45

45

45

45

45

Zadanie 4.10

45

45

45

45

45

45

45

Zadanie 4.11

45

45

45

45

45

45

45

Zadanie 4.12

45

45

45

45

45

45

45

Zadanie 4.13

45

45

45

45

45

45

45

Zadanie 4.14

45

45

45

45

45

45

45

Zadanie 4.15

46

46

46

46

46

Zadanie 4.16

46

46

46

46

46

46

46

Zadanie Prosto do matury - 1

30

Zadanie Prosto do matury - 2

30

Zadanie Prosto do matury - 3

30

30

30

Zadanie Prosto do matury - 4

30

Zadanie Prosto do matury - 5

30

55

55

55

Zadanie 5.4

55

55

55

55

55

55

55

Zadanie 5.10

56

56

56

56

56

Zadanie 5.11

56

56

56

56

56

Zadanie 5.12

56

56

56

56

56

Zadanie 5.13

56

56

56

56

56

56

56

30

Zadanie 5.15

56

56

56

56

56

57

57

Zadanie Prosto do matury - 5.1

30

Zadanie Prosto do matury – 5.2

30

Zadanie Prosto do matury – 5.3

30

Zadanie Prosto do matury – 5.4

30

Zadanie Prosto do matury – 5.5

30

63

63

63

Zadanie 6.4

63

63

63

63

63

Zadanie 6.5

63

63

63

Zadanie 6.6

65

65

65

65

65

Zadanie 6.7

65

65

65

Zadanie 6.8

65

65

65

65

Zadanie 6.10

65

65

65

65

65

Zadanie 6.12

65

65

65

65

65

Zadanie 6.13

65

65

65

65

65

65

Zadanie 6.16

65

65

65

65

65

65

65

Zadanie 6.19

65

65

65

65

65

65

Zadanie 6.21

65

65

65

65

65

Zadanie Prosto do matury – 8.1

30

103

103

103

Zadanie 7.4

103

103

103

103

103

Zadanie 7.5

103

103

103

103

103

Zadanie 7.6

103

103

103

103

103

103

Zadanie 7.8

103

103

103

Zadanie 7.9

103

103

103

103

Zadanie 7.10

103

103

103

Zadanie 7.11

103

103

103

103

103

Zadanie 7.12

103

103

103

Zadanie 7.13

103

103

103

103

103

Zadanie 7.14

103

103

Zadanie 7.15

103

103

103

103

103

103

103

Zadanie 7.16

103

103

103

103

103

103

Zadanie 7.17

103

103

103

Zadanie 7.18

103

103

103

103

Zadanie 7.21

103

103

103

103

103

103

103

86

86

86

86

86

86

86

86

86

86

Zadanie 8.11

86

86

86

86

86

Zadanie 8.12

86

86

86

86

86

86

86

86

86

87

87

Zadanie Prosto do matury – 8.1

30

Zadanie Prosto do matury – 8.2

30

Zadanie Prosto do matury – 8.3

30

Zadanie Prosto do matury – 8.4

30

Zadanie Prosto do matury – 8.5

30

95

95

95

Zadanie 9.4

95

95

95

95

95

Zadanie 9.5

95

95

95

95

95

Zadanie 9.6

95

95

95

95

95

Zadanie 9.7

95

95

95

95

95

Zadanie 9.8

96

96

96

96

96

Zadanie 9.9

96

96

96

96

96

96

97

97

97

97

97

97

97

Zadanie 9.26

97

97

97

97

97

Zadanie Prosto do matury – 9.1

30

Zadanie Prosto do matury – 9.2

30

Zadanie Prosto do matury – 9.3

30

Zadanie Prosto do matury – 9.4

30

Zadanie Prosto do matury – 9.5

30

98

98

98

98

98

98

98

98

99

99

99

99

99

99

99

99

100

100

100

100

100

100

100

100

100

100

100

100

101

101

Zadanie 10.35

101

101

101

101

101

101

101

101

101

101

101

103

103

103

Zadanie 10.62

103

103

103

103

104

104

104

104

104

104

Zadanie 10.69

104

104

104

104

Zadanie 10.71

104

104

104

Zadanie 10.72

104

104

104

104

104

Pełny spis treści