Udowodnij, że jeśli sinusy kątów pewnego trójkąta mają się do siebie jak
![]() to trójkąt jest rozwartokątny.
to trójkąt jest rozwartokątny.
Niech kąty trójkąta to
![]()
Jeżeli sin():sin():sin(
![]() ) =
) =
![]() , to boki trójkąta będą miały długości w tym samym stosunku, więc oznaczmy boki trójkąta jako
, to boki trójkąta będą miały długości w tym samym stosunku, więc oznaczmy boki trójkąta jako
![]() .
.
Teraz możemy skorzystać z drugiego twierdzenia cosinusów.
Obliczmy cos(
![]() ):
):
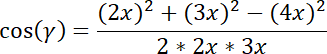
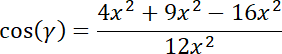
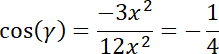
Cosinus kąta jest ujemny, więc trójkąt jest rozwartokątny.

W problemie, którego rozwiązanie jest przedstawione, przyjęliśmy, że stosunek sinusów kątów trójkąta wynosi 2:3:4. Na podstawie pierwszego twierdzenia sinusów mogliśmy wywnioskować, że długości boków trójkąta są proporcjonalne do tych samych liczb, co pozwoliło nam je oznaczyć jako
![]() .
.
Następnie, korzystając z drugiego twierdzenia cosinusów obliczyliśmy cosinus największego kąta trójkąta, jakim jest kąt
![]() na przeciwko najdłuższego boku. Wychodził on ujemny, co oznacza, że kąt
na przeciwko najdłuższego boku. Wychodził on ujemny, co oznacza, że kąt
![]() jest większy od 90 stopni, a więc trójkąt jest rozwartokątny.
jest większy od 90 stopni, a więc trójkąt jest rozwartokątny.

Zadanie 1.5
14Zadanie 1.7
14Zadanie 1.12
15Zadanie 2.4
21Zadanie 2.8
21Zadanie 2.9
21Zadanie 3.9
31Zadanie 4.4
44Zadanie 4.7
45Zadanie 4.8
45Zadanie 4.9
45Zadanie 4.10
45Zadanie 4.11
45Zadanie 4.12
45Zadanie 4.13
45Zadanie 4.14
45Zadanie 4.15
46Zadanie 4.16
46Zadanie Prosto do matury - 3
30Zadanie 5.4
55Zadanie 5.10
56Zadanie 5.11
56Zadanie 5.12
56Zadanie 5.13
56Zadanie 5.15
56Zadanie 6.4
63Zadanie 6.5
63Zadanie 6.6
65Zadanie 6.7
65Zadanie 6.8
65Zadanie 6.10
65Zadanie 6.12
65Zadanie 6.13
65Zadanie 6.16
65Zadanie 6.19
65Zadanie 6.21
65Zadanie 7.4
103Zadanie 7.5
103Zadanie 7.6
103Zadanie 7.8
103Zadanie 7.9
103Zadanie 7.10
103Zadanie 7.11
103Zadanie 7.12
103Zadanie 7.13
103Zadanie 7.14
103Zadanie 7.15
103Zadanie 7.16
103Zadanie 7.17
103Zadanie 7.18
103Zadanie 7.21
103Zadanie 8.11
86Zadanie 8.12
86Zadanie 9.4
95Zadanie 9.5
95Zadanie 9.6
95Zadanie 9.7
95Zadanie 9.8
96Zadanie 9.9
96Zadanie 9.26
97Zadanie 10.35
101Zadanie 10.62
103Zadanie 10.69
104Zadanie 10.71
104Zadanie 10.72
104
