Prosto do matury. Klasa 3. Zakres podstawowy. Podręcznik - rozwiązania i odpowiedzi

Podręcznik, Wydawnictwo: Nowa Era

Zadanie 5.10, b) - strona 56

W tym zadaniu musisz znaleźć wartości pozostałych funkcji trygonometrycznych kąta , jeśli
$\text{[math]}$ i $\text{[math]}$

Znamy wartość $\text{[math]}$ oraz że znajduje się w IV ćwiartce.
Stosując jedynkę trygonometryczną obliczamy:

$\text{[math]}$

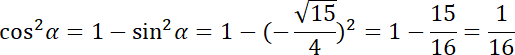
Pamiętając, że $\text{[math]}$ jest dodatnie w IV ćwiartce, mamy:

$\text{[math]}$

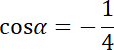
Następnie obliczamy:

$\text{[math]}$

$\text{[math]}$

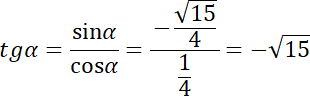
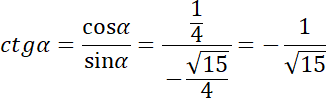
Aby obliczyć wartości pozostałych funkcji trygonometrycznych, kiedy znane jest jedno zadanie, korzystamy z identyczności trygonometrycznej, która pokazuje związki między różnymi funkcjami trygonometrycznymi. Szczególnie użyteczne jest tu równość $\text{[math]}$ , która pozwala na przejście od sinusa do cosinusa i odwrotnie. Następnie, korzystając z równań $\text{[math]}$ oraz $\text{[math]}$ , możemy znaleźć wartości tangens i cotangensa. Przy tych obliczeniach musimy pamiętać o znakach funkcji trygonometrycznych w poszczególnych ćwiartkach układu współrzędnych. Po otrzymaniu wartości, można łatwo obliczyć wartości pozostałych funkcji.

Zadanie 18, strona 86, Matematyka z kluczem. Klasa 5. Podręcznik. Część 1 - rozwiązania i odpowiedzi

Ćwiczenie 9., strona 11, Matematyka wokół nas. Klasa 6. Zeszyt ćwiczeń. Część 2 – rozwiązania i odpowiedzi

Zadanie 16, strona 111, MATeMAtyka. Klasa 3. Zbiór zadań. Zakres podstawowy i rozszerzony – rozwiązania i odpowiedzi

Zadanie 2, strona 64, Matematyka z plusem. Klasa 8. Podręcznik – rozwiązania i odpowiedzi

Zadanie co umiem? 4, strona 261, Matematyka. Klasa 6. Podręcznik - rozwiązania i odpowiedzi

Zadanie 5., strona 35, Matematyka wokół nas. Klasa 6. Zbiór zadań - rozwiązania i odpowiedzi

Zadanie 25., strona 38, Matematyka z plusem. Klasa 4. Zbiór zadań - rozwiązania i odpowiedzi

Ćwiczenie C, strona 116, Matematyka z plusem. Klasa 7. Podręcznik – rozwiązania i odpowiedzi

Zadanie 27, strona 131, Matematyka z plusem 1. Zbiór zadań dla liceum i technikum. Zakres podstawowy i rozszerzony

Zadanie Problem 2, strona 227, Matematyka wokół nas. Klasa 6. Podręcznik – rozwiązania i odpowiedzi

14

14

14

14

Zadanie 1.5

14

14

14

14

14

14

Zadanie 1.7

14

14

14

14

15

15

15

15

Zadanie 1.12

15

15

15

15

15

15

15

15

15

14

15

15

15

Zadanie Prosto do matury – 1.1

30

Zadanie Prosto do matury – 1.2

30

Zadanie Prosto do matury – 1.3

30

Zadanie Prosto do matury – 1.4

30

Zadanie Prosto do matury – 1.5

30

21

21

21

Zadanie 2.4

21

21

21

21

21

21

21

21

Zadanie 2.8

21

21

21

21

21

Zadanie 2.9

21

21

21

21

21

23

23

23

23

23

23

23

23

23

23

23

23

23

23

23

Zadanie Prosto do matury – 2.1

30

Zadanie Prosto do matury – 2.2

30

Zadanie Prosto do matury – 2.3

30

Zadanie Prosto do matury – 2.5

30

30

30

30

30

30

30

30

Zadanie 3.9

31

31

31

31

31

31

31

31

31

31

31

31

31

31

Zadanie Prosto do matury - 1

30

Zadanie Prosto do matury - 2

30

Zadanie Prosto do matury - 3

30

Zadanie Prosto do matury - 4

30

Zadanie Prosto do matury - 5

30

44

44

44

Zadanie 4.4

44

44

44

44

44

44

44

45

Zadanie 4.7

45

45

45

45

Zadanie 4.8

45

45

45

45

45

45

45

Zadanie 4.9

45

45

45

45

45

45

45

Zadanie 4.10

45

45

45

45

45

45

45

Zadanie 4.11

45

45

45

45

45

45

45

Zadanie 4.12

45

45

45

45

45

45

45

Zadanie 4.13

45

45

45

45

45

45

45

Zadanie 4.14

45

45

45

45

45

45

45

Zadanie 4.15

46

46

46

46

46

Zadanie 4.16

46

46

46

46

46

46

46

Zadanie Prosto do matury - 1

30

Zadanie Prosto do matury - 2

30

Zadanie Prosto do matury - 3

30

30

30

Zadanie Prosto do matury - 4

30

Zadanie Prosto do matury - 5

30

55

55

55

Zadanie 5.4

55

55

55

55

55

55

55

Zadanie 5.10

56

56

56

56

56

Zadanie 5.11

56

56

56

56

56

Zadanie 5.12

56

56

56

56

56

Zadanie 5.13

56

56

56

56

56

56

56

30

Zadanie 5.15

56

56

56

56

56

57

57

Zadanie Prosto do matury - 5.1

30

Zadanie Prosto do matury – 5.2

30

Zadanie Prosto do matury – 5.3

30

Zadanie Prosto do matury – 5.4

30

Zadanie Prosto do matury – 5.5

30

63

63

63

Zadanie 6.4

63

63

63

63

63

Zadanie 6.5

63

63

63

Zadanie 6.6

65

65

65

65

65

Zadanie 6.7

65

65

65

Zadanie 6.8

65

65

65

65

Zadanie 6.10

65

65

65

65

65

Zadanie 6.12

65

65

65

65

65

Zadanie 6.13

65

65

65

65

65

65

Zadanie 6.16

65

65

65

65

65

65

65

Zadanie 6.19

65

65

65

65

65

65

Zadanie 6.21

65

65

65

65

65

Zadanie Prosto do matury – 8.1

30

103

103

103

Zadanie 7.4

103

103

103

103

103

Zadanie 7.5

103

103

103

103

103

Zadanie 7.6

103

103

103

103

103

103

Zadanie 7.8

103

103

103

Zadanie 7.9

103

103

103

103

Zadanie 7.10

103

103

103

Zadanie 7.11

103

103

103

103

103

Zadanie 7.12

103

103

103

Zadanie 7.13

103

103

103

103

103

Zadanie 7.14

103

103

Zadanie 7.15

103

103

103

103

103

103

103

Zadanie 7.16

103

103

103

103

103

103

Zadanie 7.17

103

103

103

Zadanie 7.18

103

103

103

103

Zadanie 7.21

103

103

103

103

103

103

103

86

86

86

86

86

86

86

86

86

86

Zadanie 8.11

86

86

86

86

86

Zadanie 8.12

86

86

86

86

86

86

86

86

86

87

87

Zadanie Prosto do matury – 8.1

30

Zadanie Prosto do matury – 8.2

30

Zadanie Prosto do matury – 8.3

30

Zadanie Prosto do matury – 8.4

30

Zadanie Prosto do matury – 8.5

30

95

95

95

Zadanie 9.4

95

95

95

95

95

Zadanie 9.5

95

95

95

95

95

Zadanie 9.6

95

95

95

95

95

Zadanie 9.7

95

95

95

95

95

Zadanie 9.8

96

96

96

96

96

Zadanie 9.9

96

96

96

96

96

96

97

97

97

97

97

97

97

Zadanie 9.26

97

97

97

97

97

Zadanie Prosto do matury – 9.1

30

Zadanie Prosto do matury – 9.2

30

Zadanie Prosto do matury – 9.3

30

Zadanie Prosto do matury – 9.4

30

Zadanie Prosto do matury – 9.5

30

98

98

98

98

98

98

98

98

99

99

99

99

99

99

99

99

100

100

100

100

100

100

100

100

100

100

100

100

101

101

Zadanie 10.35

101

101

101

101

101

101

101

101

101

101

101

103

103

103

Zadanie 10.62

103

103

103

103

104

104

104

104

104

104

Zadanie 10.69

104

104

104

104

Zadanie 10.71

104

104

104

Zadanie 10.72

104

104

104

104

104

Pełny spis treści