W tym zadaniu wyznacz długości odcinków, na które dwusieczna kąta prostego podzieliła przeciwprostokątną, jeżeli w tym trójkącie prostokątnym przyprostokątne mają długości 6 i 8
Najpierw obliczmy długość przeciwprostokątnej korzystając z twierdzenia Pitagorasa:
![]()
Wiemy, że dwusieczna kąta prostego w trójkącie prostokątnym dzieli przeciwprostokątną w stosunku równym stosunkowi przyprostokątnych. Oznaczmy to jako następujące odcinki na przeciwprostokątnej:
![]() - mniejszy odcinek,
- mniejszy odcinek,
![]() - większy odcinek. Mamy więc:
- większy odcinek. Mamy więc:
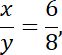
gdzie
![]()
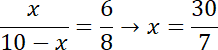
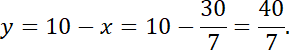

Twierdzenie Pitagorasa pozwoliło nam określić długość przeciwprostokątnej. Następnie korzystając z własności dwusiecznej w trójkącie prostokątnym. Z twierdzenia o dwusiecznej wynika, że w trójkącie prostokątnym odcinki na przeciwprostokątnej utworzone poprzez dwusieczną z kąta prostego są proporcjonalne do długości przyprostokątnych.

Zadanie 1.5
14Zadanie 1.7
14Zadanie 1.12
15Zadanie 2.4
21Zadanie 2.8
21Zadanie 2.9
21Zadanie 3.9
31Zadanie 4.4
44Zadanie 4.7
45Zadanie 4.8
45Zadanie 4.9
45Zadanie 4.10
45Zadanie 4.11
45Zadanie 4.12
45Zadanie 4.13
45Zadanie 4.14
45Zadanie 4.15
46Zadanie 4.16
46Zadanie Prosto do matury - 3
30Zadanie 5.4
55Zadanie 5.10
56Zadanie 5.11
56Zadanie 5.12
56Zadanie 5.13
56Zadanie 5.15
56Zadanie 6.4
63Zadanie 6.5
63Zadanie 6.6
65Zadanie 6.7
65Zadanie 6.8
65Zadanie 6.10
65Zadanie 6.12
65Zadanie 6.13
65Zadanie 6.16
65Zadanie 6.19
65Zadanie 6.21
65Zadanie 7.4
103Zadanie 7.5
103Zadanie 7.6
103Zadanie 7.8
103Zadanie 7.9
103Zadanie 7.10
103Zadanie 7.11
103Zadanie 7.12
103Zadanie 7.13
103Zadanie 7.14
103Zadanie 7.15
103Zadanie 7.16
103Zadanie 7.17
103Zadanie 7.18
103Zadanie 7.21
103Zadanie 8.11
86Zadanie 8.12
86Zadanie 9.4
95Zadanie 9.5
95Zadanie 9.6
95Zadanie 9.7
95Zadanie 9.8
96Zadanie 9.9
96Zadanie 9.26
97Zadanie 10.35
101Zadanie 10.62
103Zadanie 10.69
104Zadanie 10.71
104Zadanie 10.72
104
