Oblicz punkt przecięcia przekątnych prostokąta PQRS, jeśli P(-3,0) i S(-1,4), a punkt R leży na osi OX.
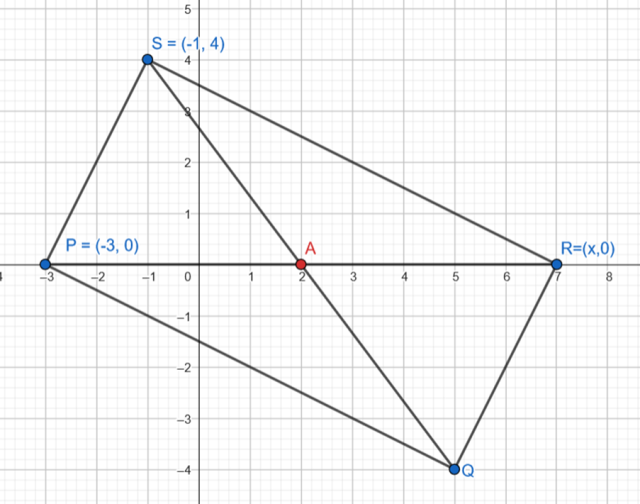
Prosta PS:
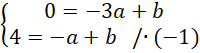
![]()
![]()
![]()
![]()
![]()
![]()
Prosta SR jest prostopadła względem prostej PS.
![]()
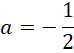
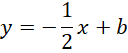
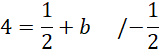
![]()
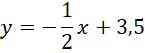
Punkt R:
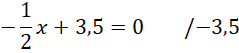
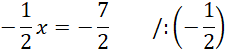
![]()
![]()
Punkt A:
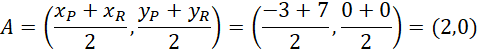

Znajdź równanie prostej PS. Współrzędne punktów P i S podstaw pod równanie kierunkowe funkcji liniowej:
![]() . Zauważ, że powstanie układ dwóch równań z dwoma niewiadomymi. Całe drugie równanie pomnóż przez -1, aby współczynniki przy
. Zauważ, że powstanie układ dwóch równań z dwoma niewiadomymi. Całe drugie równanie pomnóż przez -1, aby współczynniki przy
![]() były przeciwne, a następnie wyznacz wartość współczynnika
były przeciwne, a następnie wyznacz wartość współczynnika
![]() dodając je do siebie stronami. Podstaw wyznaczoną wartość
dodając je do siebie stronami. Podstaw wyznaczoną wartość
![]() pod jedno z początkowych równań i na tej podstawie wyznacz wartość współczynnika
pod jedno z początkowych równań i na tej podstawie wyznacz wartość współczynnika
![]() .
.
Znajdź równanie prostej SR. Zauważ, że jest ona prostopadła do prostej PS, więc ich współczynniki kierunkowe muszą być przeciwne i odwrotne, czyli spełniać warunek:
![]() .
.
Pod powyższe równanie podstaw współczynnik kierunkowy prostej PS i wyznacz wartość współczynnika prostej prostopadłej SP. Skorzystaj z tego, że do wykresu szukanej funkcji należy punkt S. Podstaw jego współrzędne w miejsce
![]() i
i
![]() w powstałym równaniu, aby obliczyć wartość współczynnika
w powstałym równaniu, aby obliczyć wartość współczynnika
![]() .
.
Wyznacz współrzędne punktu R. Zauważ, że leży on na osi OX i prostej SR, więc jego druga współrzędna jest równa 0. Na tej podstawie oblicz jego pierwszą współrzędną.
Na koniec oblicz współrzędne punktu przecięcia przekątnych prostokąta PQRS. Zauważ, że jest on środkiem odcinka PR.

Ćwiczenie 1
223Ćwiczenie 2
224Ćwiczenie 3
224Ćwiczenie 5
225Ćwiczenie 6
225Ćwiczenie 7
226Ćwiczenie 8
226Ćwiczenie 9
226Zadanie 2
227Zadanie 3
227Zadanie 4
227Zadanie 5
227Ćwiczenie 2
228Ćwiczenie 3
228Ćwiczenie 4
228Ćwiczenie 6
230Ćwiczenie 7
230Ćwiczenie 8
230Ćwiczenie 9
230Ćwiczenie 10
231Zadanie 1
231Zadanie 2
231Zadanie 3
231Zadanie 4
231Zadanie 5
231Zadanie 6
231Zadanie 7
232Zadanie 8
232Zadanie 9
232Zadanie 10
232Zadanie 12
232Zadanie 13
232Ćwiczenie 1
233Ćwiczenie 2
233Ćwiczenie 3
214Ćwiczenie 4
234Zadanie 1
235Zadanie 2
235Zadanie 3
235Zadanie 4
235Zadanie 6
236Zadanie 7
236Zadanie 10
236Zadanie 11
236Zadanie 12
236Zadanie 1
237Zadanie 2
237Zadanie 3
237Ćwiczenie 1
238Ćwiczenie 2
238Ćwiczenie 4
239Ćwiczenie 5
239Ćwiczenie 6
240Ćwiczenie 7
240Ćwiczenie 8
240Ćwiczenie 9
240Zadanie 3
241Zadanie 4
241Zadanie 5
241Zadanie 6
241Zadanie 10
242Zadanie 12
242Ćwiczenie 1
244Ćwiczenie 2
245Ćwiczenie 3
245Ćwiczenie 5
245Ćwiczenie 6
246Ćwiczenie 7
246Zadanie 1
246Zadanie 2
246Zadanie 3
246Zadanie 4
247Zadanie 5
247Zadanie 7
247Zadanie 9
247Zadanie 10
247Ćwiczenie 1
248Ćwiczenie 2
249Ćwiczenie 3
249Zadanie 1
250Zadanie 2
250Zadanie 3
250Zadanie 4
250Zadanie 5
250Zadanie 6
251Zadanie 8
251Zadanie 11
251Ćwiczenie 1
252Ćwiczenie 2
253Ćwiczenie 3
253Zadanie 1
254Zadanie 2
254Zadanie 3
254Zadanie 4
254Zadanie 5
254Zadanie 6
254Zadanie 1
255Ćwiczenie 1
256Ćwiczenie 3
257Ćwiczenie 4
257Ćwiczenie 5
258Zadanie 1
258Zadanie 2
258Zadanie 3
258Zadanie 4
258Zadanie 5
258Ćwiczenie 2
259Zadanie 1
260Zadanie 2
260Zadanie 3
261Zadanie 4
261Zadanie 6
261Zadanie 1
262Zadanie 3
262Zadanie 4
263Zadanie 5
263Zadanie 1
264Zadanie 2
264Zadanie 3
264Zadanie 4
264Zadanie 5
264Zadanie 6
264Zadanie 7
264Zadanie 8
264Zadanie 9
264Zadanie 10
264Zadanie 1
265Zadanie 2
265Zadanie 4
265Zadanie 5
265Zadanie 7
265Zadanie 2
266Zadanie 3
266
