Wewnątrz równoległoboku narysowano dwa półokręgi: średnicą jednego jest krótszy bok, a średnicą drugiego — dłuższy bok równoległoboku. W tym zadaniu musisz wykazać, że punkt przecięcia tych półokręgów różny od wierzchołka równoległoboku należy do jednej z przekątnych tego równoległoboku.
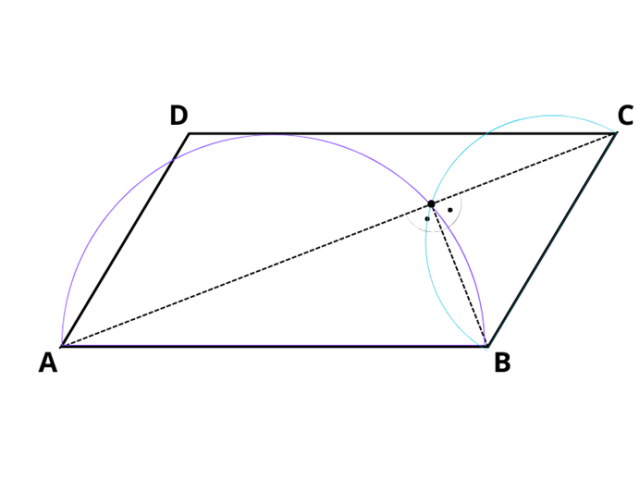
Trójkąt oparty na średnicy jest trójkątem prostokątnym
![]()
![]()
![]() punkty A, P, C są współliniowe.
punkty A, P, C są współliniowe.

Trójkąt oparty na średnicy jest trójkątem prostokątnym.

Zadanie 4.2
76Zadanie 4.5
76Zadanie 4.8
77Zadanie 4.9
77Zadanie 4.10
77Zadanie 4.11
78Zadanie 4.12
78Zadanie 4.13
78Zadanie 4.14
78Zadanie 4.19
79Zadanie 4.20
79Zadanie 4.21
79Zadanie 4.22
80Zadanie 4.23
80Zadanie 4.24
80Zadanie 4.25
80Zadanie 4.26
80Zadanie 4.27
80Zadanie 4.34
81Zadanie 4.37
81Zadanie 4.40
81Zadanie 4.41
82Zadanie 4.46
82Zadanie 4.47
82Zadanie 4.48
83Zadanie 4.52
83Zadanie 4.56
84Zadanie 4.57
84Zadanie 4.58
84Zadanie 4.59
84Zadanie 4.64
85Zadanie 4.65
85Zadanie 4.67
85Zadanie 4.68
86Zadanie 4.69
87Zadanie 4.70
87Zadanie 4.71
87Zadanie 4.72
87Zadanie 4.73
87Zadanie 4.87
89Zadanie 4.91
89Zadanie 4.93
90Zadanie 4.98
90Zadanie 4.99
91Zadanie 4.102
91Zadanie 4.105
91Zadanie 4.107
91Zadanie 4.108
92Zadanie 4.109
92Zadanie 4.111
92Zadanie 4.122
93Zadanie 4.124
93Zadanie 4.126
94Zadanie 4.127
94Zadanie 4.131
94Zadanie 4.132
94Zadanie 4.138
95Zadanie 4.139
95Zadanie 4.140
95Zadanie 4.141
95Zadanie 4.142
95Zadanie 4.143
96Zadanie 4.144
96Zadanie 17
98Zadanie 19
99Zadanie 21
99Zadanie 22
99Zadanie 24
95Zadanie 26
100Zadanie 27
100Zadanie 28
100Zadanie 29
100Zadanie 30
100
