Boki trójkąta mają długość: 15, 20, 25. W tym zadaniu musisz obliczyć długość odcinka dwusiecznej tego trójkąta poprowadzonej z wierzchołka: największego kąta.
![]() trójkąt jest prostokątny
trójkąt jest prostokątny
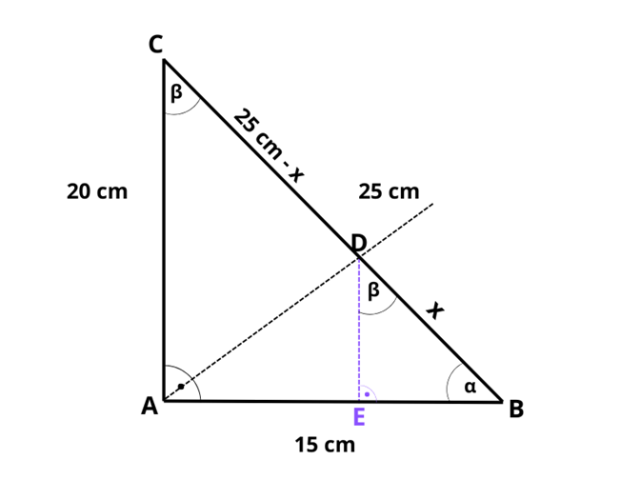
Pamiętaj, o twierdzeniu o podziale kąta wewnętrznego przez dwusieczną, dzięki czemu możemy zapisać stosunki boków trójkątów ADB i ACD. Zgodnie z tym:
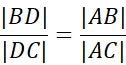
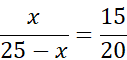
20x = 375 – 15x / + 15x
35x = 375 /: 35
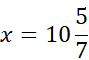
Zauważ, że trójkąty EBD oraz ABC są podobne na podstawie cechy kąt-kąt-kąt (KKK). Są to kąty: α, β oraz 90°. Są one podobne do siebie w skali k, a więc:
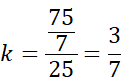
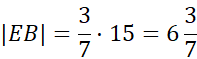
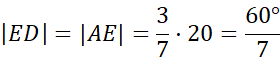
Trójkąt ma kąty 45°, 45°, 90°
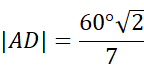

Zauważ, że trójkąt ABC jest prostokątny. Wykorzystaj twierdzenie o dwusiecznej kąta wewnętrznego w trójkącie: dwusieczna kąta wewnętrznego w trójkącie dzieli przeciwległy bok proporcjonalnie do długości pozostałych boków. Następnie znajdź trójkąty podobne i oblicz ich skalę. Na podstawie skali znajdź boki trójkąta EBD.

Zadanie 4.2
76Zadanie 4.5
76Zadanie 4.8
77Zadanie 4.9
77Zadanie 4.10
77Zadanie 4.11
78Zadanie 4.12
78Zadanie 4.13
78Zadanie 4.14
78Zadanie 4.19
79Zadanie 4.20
79Zadanie 4.21
79Zadanie 4.22
80Zadanie 4.23
80Zadanie 4.24
80Zadanie 4.25
80Zadanie 4.26
80Zadanie 4.27
80Zadanie 4.34
81Zadanie 4.37
81Zadanie 4.40
81Zadanie 4.41
82Zadanie 4.46
82Zadanie 4.47
82Zadanie 4.48
83Zadanie 4.52
83Zadanie 4.56
84Zadanie 4.57
84Zadanie 4.58
84Zadanie 4.59
84Zadanie 4.64
85Zadanie 4.65
85Zadanie 4.67
85Zadanie 4.68
86Zadanie 4.69
87Zadanie 4.70
87Zadanie 4.71
87Zadanie 4.72
87Zadanie 4.73
87Zadanie 4.87
89Zadanie 4.91
89Zadanie 4.93
90Zadanie 4.98
90Zadanie 4.99
91Zadanie 4.102
91Zadanie 4.105
91Zadanie 4.107
91Zadanie 4.108
92Zadanie 4.109
92Zadanie 4.111
92Zadanie 4.122
93Zadanie 4.124
93Zadanie 4.126
94Zadanie 4.127
94Zadanie 4.131
94Zadanie 4.132
94Zadanie 4.138
95Zadanie 4.139
95Zadanie 4.140
95Zadanie 4.141
95Zadanie 4.142
95Zadanie 4.143
96Zadanie 4.144
96Zadanie 17
98Zadanie 19
99Zadanie 21
99Zadanie 22
99Zadanie 24
95Zadanie 26
100Zadanie 27
100Zadanie 28
100Zadanie 29
100Zadanie 30
100
