W trójkącie ABC, w którym
![]() oraz |AC|<|BC|, zaznaczono środek ciężkości S i spodek D wysokości CD. W tym zadaniu musisz wykazać, że jeśli |AD| = 3 oraz |BD| = 6, to odcinek DS jest równoległy do boku AC, a jego długość jest równa
oraz |AC|<|BC|, zaznaczono środek ciężkości S i spodek D wysokości CD. W tym zadaniu musisz wykazać, że jeśli |AD| = 3 oraz |BD| = 6, to odcinek DS jest równoległy do boku AC, a jego długość jest równa
![]() .
.
Środkowa dzielą się w stosunku 2:1. Niech E będzie spodkiem wysokości środkowej BS. To znaczy, że
![]() . Zauważmy, że
. Zauważmy, że
![]() . Zatem
. Zatem
![]() . Z twierdzenia odwrotnego do twierdzenia Talesa wynika wtedy, że proste DS i AE są równoległe.
. Z twierdzenia odwrotnego do twierdzenia Talesa wynika wtedy, że proste DS i AE są równoległe.
Z ustalonego podobieństwa można wyliczyć
![]() jako
jako
![]() czyli
czyli
![]() gdyż E dzieli odcinek AC na pół. Używając wzoru
gdyż E dzieli odcinek AC na pół. Używając wzoru
![]() gdzie
gdzie
![]() to długości na jakie dzieli wysokość bok
to długości na jakie dzieli wysokość bok
![]() , w tym przypadku
, w tym przypadku
![]() dostajemy
dostajemy
![]() .
.
Teraz możemy policzyć bok AC z twierdzenia Pitagorasa:
![]() więc
więc
![]() .
.

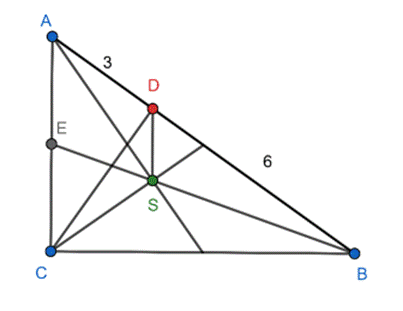
W rozwiązaniu musisz skorzystać z odwrotnego twierdzenia do twierdzenia Talesa: dwie proste wychodzą ze wspólnego punktu (tutaj z punktu B wychodzą proste BA i BE) i przecinane są dwoma prostymi (tutaj prostymi DS i AE) w taki sposób, że zachodzi odpowiednia proporcja, to proste przecinające są równoległe.
Tutaj „odpowiednia proporcja” to
![]() wykorzystująca fakt, że punkt S dzieli środkową w takim samym stosunku (2:1) jak odcinki 6 i 3 w założeniu zadania.
wykorzystująca fakt, że punkt S dzieli środkową w takim samym stosunku (2:1) jak odcinki 6 i 3 w założeniu zadania.
Dalej wyliczenie długości
![]() polega na skorzystaniu ze wzoru
polega na skorzystaniu ze wzoru
![]() , i twierdzeniu Pitagorasa dla małego trójkąta prostokątnego.
, i twierdzeniu Pitagorasa dla małego trójkąta prostokątnego.

Zadanie 2
122Zadanie 5
122Zadanie 8
123Zadanie 9
123Zadanie 10
123Zadanie 11
124Zadanie 12
124Zadanie 13
124Zadanie 14
124Zadanie 19
125Zadanie 20
125Zadanie 21
125Zadanie 22
126Zadanie 23
126Zadanie 24
126Zadanie 25
126Zadanie 26
126Zadanie 27
126Zadanie 34
127Zadanie 37
127Zadanie 40
128Zadanie 42
128Zadanie 44
128Zadanie 45
128Zadanie 46
129Zadanie 51
129Zadanie 52
129Zadanie 53
129Zadanie 57
130Zadanie 61
131Zadanie 62
131Zadanie 63
131Zadanie 64
131Zadanie 69
132Zadanie 70
132Zadanie 75
132Zadanie 78
133Zadanie 79
134Zadanie 80
134Zadanie 81
134Zadanie 82
135Zadanie 83
135Zadanie 84
135Zadanie 103
137Zadanie 107
138Zadanie 109
138Zadanie 113
139Zadanie 118
140Zadanie 119
140Zadanie 122
140Zadanie 125
140Zadanie 127
141Zadanie 128
141Zadanie 129
141Zadanie 131
141Zadanie 137
142Zadanie 146
143Zadanie 148
143Zadanie 150
143Zadanie 151
143Zadanie 155
144Zadanie 156
144Zadanie 162
145Zadanie 163
145Zadanie 164
145Zadanie 165
145Zadanie 166
145Zadanie 167
145Zadanie 168
145Zadanie 169
146Zadanie 171
146Zadanie 172
146Zadanie 173
146Zadanie 174
147Zadanie 17
149Zadanie 19
149Zadanie 21
150Zadanie 22
150Zadanie 24
150Zadanie 26
150Zadanie 27
151Zadanie 28
151Zadanie 29
151Zadanie 30
151Zadanie 32
151Zadanie 37
152
