W trójkącie ABC poprowadzono środkową AD. W tym zadaniu musisz wykazać, że jeśli suma miar kątów DAC i ACB jest równa mierze kąta ADC, to trójkąt ABC jest równoramienny.
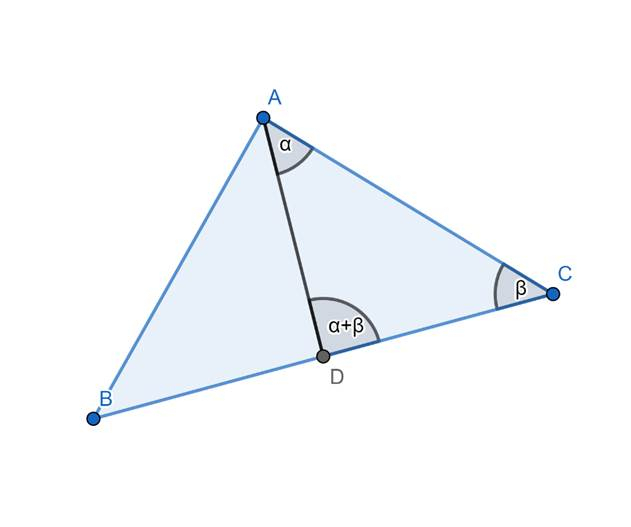
Oznaczmy miary kątów DAC
![]() oraz ACB
oraz ACB
![]() . Wtedy z sumy kątów w trójkącie
. Wtedy z sumy kątów w trójkącie
![]() wychodzi
wychodzi
![]() co daje
co daje
![]() .
.
Skoro kąt
![]() jest prosty, to kąt przyległy
jest prosty, to kąt przyległy
![]() też. Mamy dwa kąty prostokątne, które mają równe przyprostokątne (
też. Mamy dwa kąty prostokątne, które mają równe przyprostokątne (
![]() mają wspólną, a
mają wspólną, a
![]() bo
bo
![]() to środek odcinka
to środek odcinka
![]() z założenia że
z założenia że
![]() to środkowa) – z tego wynika, że trójkąty
to środkowa) – z tego wynika, że trójkąty
![]() i
i
![]() są przystające (np. reguła bok - kąt - bok) więc boki
są przystające (np. reguła bok - kąt - bok) więc boki
![]() i
i
![]() też są równe – czyli udowodniliśmy, że trójkąt
też są równe – czyli udowodniliśmy, że trójkąt
![]() jest równoramienny.
jest równoramienny.

W tym zadaniu musisz dojść do tego, że kąt
![]() jest prosty. Wychodzi to z sumy kątów w trójkącie
jest prosty. Wychodzi to z sumy kątów w trójkącie
![]() . Zawsze warto spojrzeć na sumę kątów w trójkącie jeśli znane są jakieś zależności między tymi kątami.
. Zawsze warto spojrzeć na sumę kątów w trójkącie jeśli znane są jakieś zależności między tymi kątami.

Zadanie 2
122Zadanie 5
122Zadanie 8
123Zadanie 9
123Zadanie 10
123Zadanie 11
124Zadanie 12
124Zadanie 13
124Zadanie 14
124Zadanie 19
125Zadanie 20
125Zadanie 21
125Zadanie 22
126Zadanie 23
126Zadanie 24
126Zadanie 25
126Zadanie 26
126Zadanie 27
126Zadanie 34
127Zadanie 37
127Zadanie 40
128Zadanie 42
128Zadanie 44
128Zadanie 45
128Zadanie 46
129Zadanie 51
129Zadanie 52
129Zadanie 53
129Zadanie 57
130Zadanie 61
131Zadanie 62
131Zadanie 63
131Zadanie 64
131Zadanie 69
132Zadanie 70
132Zadanie 75
132Zadanie 78
133Zadanie 79
134Zadanie 80
134Zadanie 81
134Zadanie 82
135Zadanie 83
135Zadanie 84
135Zadanie 103
137Zadanie 107
138Zadanie 109
138Zadanie 113
139Zadanie 118
140Zadanie 119
140Zadanie 122
140Zadanie 125
140Zadanie 127
141Zadanie 128
141Zadanie 129
141Zadanie 131
141Zadanie 137
142Zadanie 146
143Zadanie 148
143Zadanie 150
143Zadanie 151
143Zadanie 155
144Zadanie 156
144Zadanie 162
145Zadanie 163
145Zadanie 164
145Zadanie 165
145Zadanie 166
145Zadanie 167
145Zadanie 168
145Zadanie 169
146Zadanie 171
146Zadanie 172
146Zadanie 173
146Zadanie 174
147Zadanie 17
149Zadanie 19
149Zadanie 21
150Zadanie 22
150Zadanie 24
150Zadanie 26
150Zadanie 27
151Zadanie 28
151Zadanie 29
151Zadanie 30
151Zadanie 32
151Zadanie 37
152
