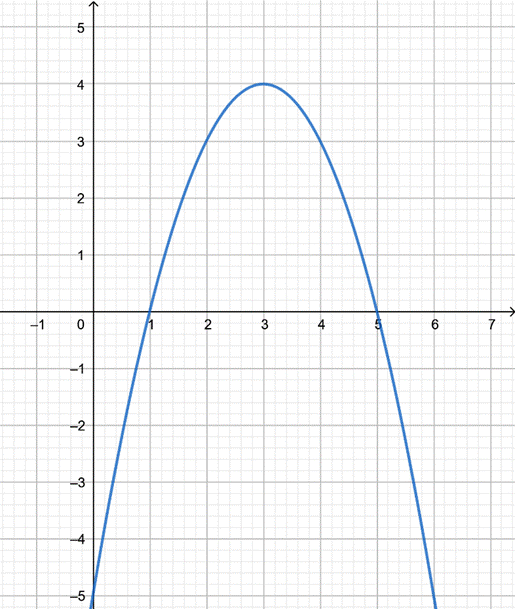
Wyznacz współrzędne wierzchołka paraboli będącej wykresem funkcji f, miejsca zerowe funkcji, współrzędne przecięcia wykresu z osią OY oraz współrzędne punktu symetrycznego do niej względem osi symetrii paraboli. Narysuj wykres funkcji.
![]()
W(3, 4)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
OY = (0, -5)
![]()
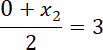
![]()
![]()
P(6, -5)

Wzór funkcji w postaci kanonicznej ma postać
![]() gdzie p i q to współrzędne wierzchołka paraboli. Przyrównaj funkcję kwadratową do zera, aby znaleźć jej miejsca zerowe. Aby obliczyć punkt OY, podstaw za x zero. Użyj wzoru
gdzie p i q to współrzędne wierzchołka paraboli. Przyrównaj funkcję kwadratową do zera, aby znaleźć jej miejsca zerowe. Aby obliczyć punkt OY, podstaw za x zero. Użyj wzoru
![]() , aby znaleźć punkt symetryczny do danego punktu.
, aby znaleźć punkt symetryczny do danego punktu.

Zadanie 6.1
150Zadanie 6.2
150Zadanie 6.4
150Zadanie 6.6
151Zadanie 6.7
151Zadanie 6.8
151Zadanie 6.9
151Zadanie 6.10
152Zadanie 6.11
152Zadanie 6.12
152Zadanie 6.13
152Zadanie 6.14
152Zadanie 6.15
153Zadanie 6.16
153Zadanie 6.17
153Zadanie 6.18
153Zadanie 6.19
153Zadanie 6.20
152Zadanie 6.21
153Zadanie 6.22
153Zadanie 6.23
154Zadanie 6.24
154Zadanie 6.25
154Zadanie 6.26
154Zadanie 6.27
155Zadanie 6.28
155Zadanie 6.29
155Zadanie 6.30
155Zadanie 6.34
156Zadanie 6.35
156Zadanie 6.36
156Zadanie 6.37
157Zadanie 6.38
157Zadanie 6.39
157Zadanie 6.40
157Zadanie 6.41
157Zadanie 6.49
158Zadanie 6.50
158Zadanie 6.51
158Zadanie 6.52
159Zadanie 6.53
159Zadanie 6.54
159Zadanie 6.55
159Zadanie 6.56
159Zadanie 6.57
159Zadanie 6.58
160Zadanie 6.59
160Zadanie 6.60
160Zadanie 6.61
160Zadanie 6.62
160Zadanie 5.
161Zadanie 11.
162Zadanie 12.
162Zadanie 14.
162Zadanie 15.
162Zadanie 16.
162Zadanie 17.
163Zadanie 19.
163Zadanie 20.
163
