W tym zadaniu należy przeczytać twierdzenie w ramce oraz udowodnić, że iloraz liczby wymiernej różnej od zera przez liczbę niewymierną jest liczbą niewymierną.
Twierdzenie:
Jeśli a jest liczbą niewymierną i w jest liczbą wymierną,
to a - w jest liczbą niewymierną.
Dowód (metodą nie wprost):
Przypuśćmy, że liczba x = a - w jest wymierna.
Wówczas także liczba x + w jest wymierna (bo suma liczb wymiernych jest liczbą wymierną).
Ponieważ x + w = a - w + w = a, więc liczba a musiałaby być wymierna, co jest sprzeczne z założeniem.
Załóżmy, że istnieją liczby wymierne a, c
![]() oraz liczba niewymierna x, które spełniają równość:
oraz liczba niewymierna x, które spełniają równość:
![]() .
.
Skoro a jest wymierna to można ją zapisać w postaci ułamka zwykłego:
![]() . Analogicznie z liczbą c:
. Analogicznie z liczbą c:
![]() .
.
![]()
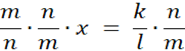
![]() – ta równość mówi, że x jest wymierne, co jest sprzeczne z założeniem. Zatem iloraz liczby wymiernej i niewymiernej jest liczbą niewymierną.
– ta równość mówi, że x jest wymierne, co jest sprzeczne z założeniem. Zatem iloraz liczby wymiernej i niewymiernej jest liczbą niewymierną.

Iloraz (dzielenie) to mnożenie przez odwrotność, a iloczyn dwóch licz wymiernych jest liczbą wymierną. Natomiast iloczyn liczby wymiernej i niewymiernej jest liczbą niewymierną. Zatem jeżeli taka zależność zachodzi dla iloczynu, zachodzi również dla ilorazu.

Zadanie 1
25Zadanie 2
25Zadanie 3
25Zadanie 4
25Zadanie 5
26Zadanie 6
26Zadanie 7
26Zadanie 8
26Zadanie 9
27Zadanie 10
27Zadanie 11
27Zadanie 12
27Zadanie 13
28Zadanie 14
28Zadanie 15
28Zadanie 16
28Zadanie 17
28Zadanie 18
28Zadanie 19
29Zadanie 20
29Zadanie 21
29Zadanie 22
29Zadanie 23
29Zadanie 24
29Zadanie 25
30Pytanie 26
30Zadanie 27
30Zadanie 29
30Zadanie 30
30Zadanie 31
30Zadanie 32
31Zadanie 33
31Zadanie 34
31Zadanie 35
31Zadanie 36
31Zadanie 37
31Zadanie 38
32Zadanie 39
32Zadanie 40
32Zadanie 41
32Zadanie 42
32Zadanie 43
32Zadanie 44
32Zadanie 45
32Zadanie 46
33Zadanie 47
33Zadanie 48
33Zadanie 49
33Zadanie 50
33Zadanie 51
33Zadanie 52
34Zadanie 53
34Zadanie 56
34Zadanie 57
34Zadanie 58
34Zadanie 59
35Zadanie 60
35Zadanie 61
35Zadanie 62
35Zadanie 63
36Zadanie 64
36Zadanie 65
36Zadanie 66
36Zadanie 67
36Zadanie 6
36Zadanie 7
36Zadanie 8
37Zadanie 9
37Zadanie 15
38Pytanie 17
38
