
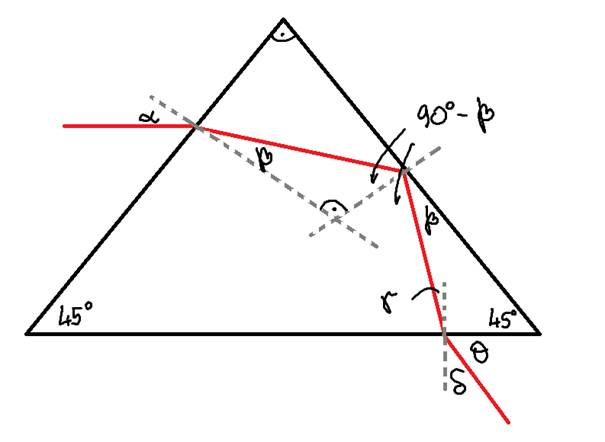
Promień światła monochromatycznego padającego na pryzmat jest równoległy do podstawy, zatem wnioskujemy, że wymiar kąta α to 45˚:
![]()
Światło biegnie równolegle do podstawy w powietrzu (dokładniej mówiąc w próżni, która pozbawiona jest zanieczyszczających powietrze pierwiastków, które gęstość optyczną zwiększają), którego współczynnik załamania jest 1, zatem nic nie zmienia.
W celu wyliczenia kąta załamania β korzystamyz prawa Snelliusa, z którego wynika:
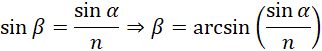
![]()
Wynika z tego, że załamany promień światła w pryzmacie, który pada na ścianę wewnątrz pryzmatu, tworzy kąt:
![]()
Do normalnej.
Patrząc po współczynniku załamania światła w pryzmacie, jest to szkło kwarcowe, dla którego kąt graniczny to ok. 43˚, zatem stawiamy tezę, jakoby na tej ścianie miało nastąpić całkowite wewnętrzne odbicie, jednak ponieważ jest to tylko teza, to sprawdzimy jej poprawność, korzystając z definicji kąta granicznego:
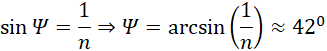
Zatem według przypuszczeń na ścianie nastąpi całkowite wewnętrzne odbicie, gdyż kąt padania na ścianę jest większy niż graniczny kąt dla pryzmatu.
Następnie promień świetlny kieruje się w stronę podstawy pryzmaty, by paść na nią pod kątem γ. Z geometrycznej analizy rysunku wyliczamy ten kąt:
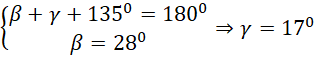
Promień ten załamuje się na podstawie pryzmatu, by ponownie wrócić do powietrza (próżni) o współczynniku załamania 1.
Na mocy prawa Snelliusa wyliczamy kąt załamania δ:
![]()
![]()