Należy udowodnić twierdzenie na podstawie definicji, które są zawarte w podręczniku.
Wiemy, że wektory
![]() i
i
![]() , gdzie
, gdzie
![]() i
i
![]() są przeciwne, gdy suma wektorów
są przeciwne, gdy suma wektorów
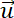 i
i
![]() to wektor zerowy, czyli ux + vx = 0, a także uy + vy = 0
to wektor zerowy, czyli ux + vx = 0, a także uy + vy = 0
Na podstawie równań zauważ, że:
Następnie sprawdzamy, czy wektory
![]() i
i
![]() mają tę samą długość:
mają tę samą długość:
Więc:
![]()
Sprawdźmy, czy istnieje liczba rzeczywista, która po wymnożeniu przez jeden wektor da nam wektor drugi.
Skoro
![]() i
i
![]() i
i
![]() ,
,
![]() to:
to:
![]() i
i
![]()
![]()
![]()
Co dowodzi, że istnieje liczba, która pomnożona przez wektor pierwszy, da nam wektor drugi, więc wektory są równoległe.
Dodatkowo widzimy, że liczba ta to–1, z kolei (–1) < 0, więc wektory
![]() i
i
![]() mają przeciwne zwroty.
mają przeciwne zwroty.

Należy skorzystać z twierdzeń: na przeciwność wektorów, na równoległość wektorów, na zwrot wektorów, a także zastosuj wzór na długość wektorów.

Zadanie 1.
10Zadanie 2.
10Zadanie 3.
10Zadanie 4.
10Zadanie 5.
10Ćwiczenie 2.
12Ćwiczenie 5.
17Ćwiczenie 6.
18Zadanie 1.
18Zadanie 4.
18Zadanie 5.
18Zadanie 6.
18Zadanie 7.
19Zadanie 8.
19Zadanie 9.
19Zadanie 10.
19Zadanie 11.
19Zadanie 12.
19Zadanie 13.
19Zadanie 14.
19Zadanie 15.
19Ćwiczenie 4.
23Zadanie 1.
23Zadanie 2.
24Zadanie 3.
24Zadanie 4.
24Zadanie 10.
24Zadanie 11.
24Zadanie 1.
27Zadanie 3.
27Zadanie 4.
27Zadanie 5.
27Zadanie 6.
27Zadanie 7.
27Zadanie 8.
27Zadanie 1.
31Zadanie 2.
31Zadanie 3.
31Zadanie 4.
31Zadanie 5.
31Zadanie 6.
31Zadanie 7.
31Zadanie 1.
34Zadanie 2.
34Zadanie 6.
34Ćwiczenie 1.
35Zadanie 1.
37Zadanie 2.
37Zadanie 16.
39Zadanie 17.
40Zadanie 18.
40Zadanie 19.
40Zadanie 20.
40Zadanie 21.
40Zadanie 22.
40Zadanie 23.
40Zadanie 24.
40
