W tym zadaniu należy narysować wykres (przekształcić wykres f przez symetrię osiową względem osi OX), wyznaczyć dziedziny i zbiory wartości funkcji f i g.
Wykres funkcji g(x) = –f(x)
Dziedzina funkcji f(x): x ⋲ <–3,5), a zbiór wartości f(x): y ⋲ <–3,2>
Dziedzina funkcji g(x): x ⋲ <–3,5), a zbiór wartości g(x): y ⋲ <–2,3>
Df = Dg
Wykres funkcji g(x) = –f(x)
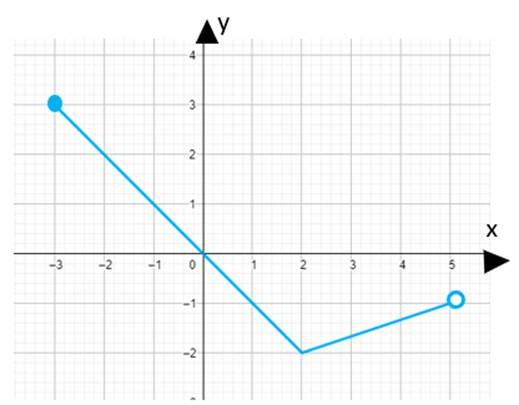

Aby rozwiązać to zadanie, należy skorzystać z twierdzenia na symetrię osiową względem osi OX dla wykresów funkcji. Zauważmy, że dziedziny tych funkcji będą takie same, natomiast zbiór wartości funkcji g będzie przeciwny w stosunku do zbioru wartości wykresu funkcji f.

Zadanie 1.
10Zadanie 2.
10Zadanie 3.
10Zadanie 4.
10Zadanie 5.
10Ćwiczenie 2.
12Ćwiczenie 5.
17Ćwiczenie 6.
18Zadanie 1.
18Zadanie 4.
18Zadanie 5.
18Zadanie 6.
18Zadanie 7.
19Zadanie 8.
19Zadanie 9.
19Zadanie 10.
19Zadanie 11.
19Zadanie 12.
19Zadanie 13.
19Zadanie 14.
19Zadanie 15.
19Ćwiczenie 4.
23Zadanie 1.
23Zadanie 2.
24Zadanie 3.
24Zadanie 4.
24Zadanie 10.
24Zadanie 11.
24Zadanie 1.
27Zadanie 3.
27Zadanie 4.
27Zadanie 5.
27Zadanie 6.
27Zadanie 7.
27Zadanie 8.
27Zadanie 1.
31Zadanie 2.
31Zadanie 3.
31Zadanie 4.
31Zadanie 5.
31Zadanie 6.
31Zadanie 7.
31Zadanie 1.
34Zadanie 2.
34Zadanie 6.
34Ćwiczenie 1.
35Zadanie 1.
37Zadanie 2.
37Zadanie 16.
39Zadanie 17.
40Zadanie 18.
40Zadanie 19.
40Zadanie 20.
40Zadanie 21.
40Zadanie 22.
40Zadanie 23.
40Zadanie 24.
40
