Należy przerysować funkcję, narysować funkcję, która jest przesunięta w stosunku do funkcji początkowej, określić przedziały, kiedy wartości rosną, maleją oraz są stałe.
Rysunek pomocniczy
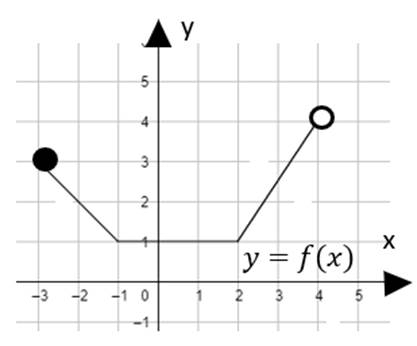
Funkcja f jest malejąca w przedziale x ⋲ (–3,–1>, funkcja jest stała w przedziale x ⋲ (–1,2>, funkcja jest rosnąca x ⋲ (2,4).
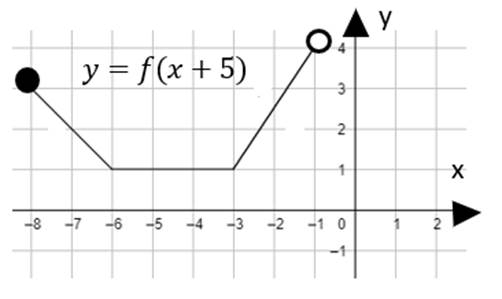
Funkcja f(x + 5) jest malejąca w przedziale x ⋲ <–8, – 6>, funkcja jest stała w przedziale x ⋲
(–6,–3>, funkcja jest rosnąca dla x ⋲ (–3,–1).

Należy narysować funkcję f(x + 5) która jest przesunięciem funkcji f o wektor [–5,0] Określić przedziały, kiedy wartości rosną, maleją oraz są stałe. Monotoniczność funkcji to nic innego jak zweryfikowanie, na jakich przedziałach funkcja rośnie (rosną jej wartości y), maleje (maleją jej wartości y), oraz na jakim przedziale punkty x przyjmują stałą wartość na osi y. Dodatkowo zauważyć można, że monotoniczność tych dwóch funkcji różni się również o wektor [–5,0].

Zadanie 1.
10Zadanie 2.
10Zadanie 3.
10Zadanie 4.
10Zadanie 5.
10Ćwiczenie 2.
12Ćwiczenie 5.
17Ćwiczenie 6.
18Zadanie 1.
18Zadanie 4.
18Zadanie 5.
18Zadanie 6.
18Zadanie 7.
19Zadanie 8.
19Zadanie 9.
19Zadanie 10.
19Zadanie 11.
19Zadanie 12.
19Zadanie 13.
19Zadanie 14.
19Zadanie 15.
19Ćwiczenie 4.
23Zadanie 1.
23Zadanie 2.
24Zadanie 3.
24Zadanie 4.
24Zadanie 10.
24Zadanie 11.
24Zadanie 1.
27Zadanie 3.
27Zadanie 4.
27Zadanie 5.
27Zadanie 6.
27Zadanie 7.
27Zadanie 8.
27Zadanie 1.
31Zadanie 2.
31Zadanie 3.
31Zadanie 4.
31Zadanie 5.
31Zadanie 6.
31Zadanie 7.
31Zadanie 1.
34Zadanie 2.
34Zadanie 6.
34Ćwiczenie 1.
35Zadanie 1.
37Zadanie 2.
37Zadanie 16.
39Zadanie 17.
40Zadanie 18.
40Zadanie 19.
40Zadanie 20.
40Zadanie 21.
40Zadanie 22.
40Zadanie 23.
40Zadanie 24.
40
