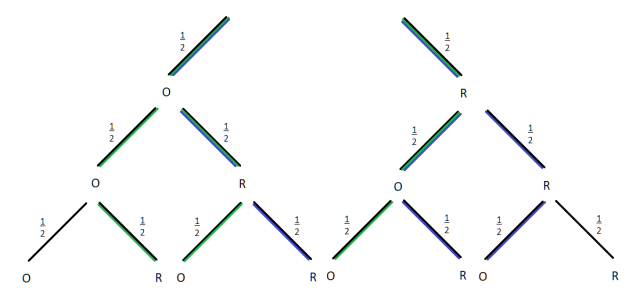
W tym zadaniu musisz podać powód, dla którego przy rzucaniu monetą prawdopodobieństwo wyrzucenia dwóch orłów i jednej reszki oraz dwóch reszek i jednego orła są równe, a także musisz podać, ile wynoszą te prawdopodobieństwa.
A – wypadnięcie dwóch orłów i jednej reszki (kolor zielony)
B – wypadnięcie jednego orła i dwóch reszek (kolor niebieski)
![]()
![]()
![]()

Ponieważ doświadczenie losowe jest wieloetapowe, w tym zadaniu musisz narysować drzewko. Każdy poziom drzewka będzie odpowiadał kolejnemu rzutowi monetą. Możesz wyrzucić albo orła, albo reszkę i te przypadki zaznaczasz jako gałęzie. Prawdopodobieństwo wyrzucenia orła wynosi zawsze jedna druga i podobnie dla reszki, co wynika z klasycznej definicji prawdopodobieństwa. Gdy już narysujesz drzewo zaznacz te zdarzenia, których prawdopodobieństwo będziesz liczył oraz wszystkie gałęzie po drodze. Dla obu zdarzeń drzewko będzie wyglądało tak samo, więc możesz zaznaczyć je oba na jednym drzewku. Na koniec przemnóż przez siebie prawdopodobieństwa na poszczególnych gałęziach oraz dodaj do siebie uzyskane wyniki z różnych gałęzi.

Ćwiczenie A.
43Przykład 1.
43Zadanie 1.
46Zadanie 2.
46Zadanie 4.
46Zadanie 5.
47Zadanie 6.
47Zadanie 7.
47Zadanie 12.
48Zadanie 16.
49Zadanie 18.
49Zadanie 20.
50Zadanie 1.
53Zadanie 2.
53Zadanie 3.
53Zadanie 6.
54Zadanie 7.
54Zadanie 10.
54Ćwiczenie A.
57Zadanie 1.
61Zadanie 2.
61Zadanie 4.
61Zadanie 5.
61Zadanie 7.
62Zadanie 8.
62Zadanie 10.
62Zadanie 11.
62Zadanie 12.
62Zadanie 15.
63Zadanie 17.
63Zadanie 18.
63Zadanie 1.
67Zadanie 2.
67Zadanie 3.
68Zadanie 5.
68Zadanie 12.
69Ćwiczenie A.
70Przykład 2.
73Zadanie 3.
74Zadanie 4.
74Zadanie 5.
75Zadanie 6.
75Zadanie 7.
75Zadanie 8.
75Zadanie 9.
75Zadanie 10.
75Zadanie 11.
76Zadanie 12.
76Zadanie 13.
76Zadanie 15.
77Zadanie 16.
77Zadanie 22.
77Zadanie 23.
78Zadanie 24.
78Zadanie 25.
78Zadanie 1.
81Zadanie 2.
81Zadanie 3.
81Zadanie 4.
81Zadanie 5.
82Zadanie 6.
82Zadanie 7.
82Zadanie 8.
82Zadanie 9.
82Zadanie 10.
83Zadanie 11.
83Zadanie 12.
83Zadanie 1.
84Zadanie 3.
84Zadanie 6.
84Zadanie 7.
84Zadanie 8.
84Zadanie 10.
84
