W tym zadaniu musisz obliczyć prawdopodobieństwo, że przy rzucie dwiema kostkami sześciennymi, na przynajmniej jednej wypadnie jedno oczko.
A – na przynajmniej jednej kostce wypadła jedynka
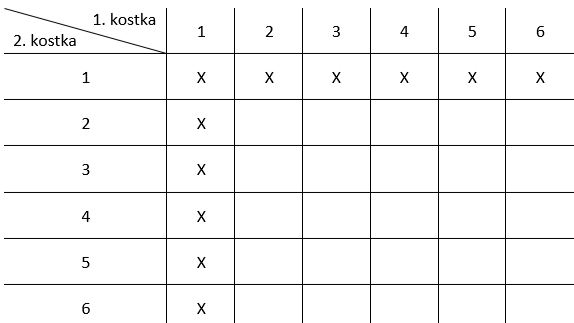
N = 6 ∙ 6 = 36
nA = 11
![]()
Odp.: Prawdopodobieństwo, że na przynajmniej jednej wyrzuconej kostce będzie jedynka wynosi ![]()

Na początku dobrze jest określić co jest tutaj zdarzeniem losowym. Jest to wyrzucenie przynajmniej na jednej kostce jedynki. Najlepszym rozwiązaniem tutaj jest narysowanie tabeli z wszystkimi możliwymi wynikami tych rzutów. Następnie zaznacz które z tych kombinacji spełniają warunek z zadania. Zauważ, że cała tabela reprezentuje przestrzeń zdarzeń elementarnych, więc musisz policzyć, ile jest komórek w tabeli. Najszybciej to zrobisz przez pomnożenie ilości wierszy i komórek. Natomiast zdarzeniem losowym będą zaznaczone przez ciebie rzuty i także musisz policzyć, ile ich jest. Dalej korzystasz z klasycznej definicji prawdopodobieństwa.

Ćwiczenie A.
43Przykład 1.
43Zadanie 1.
46Zadanie 2.
46Zadanie 4.
46Zadanie 5.
47Zadanie 6.
47Zadanie 7.
47Zadanie 12.
48Zadanie 16.
49Zadanie 18.
49Zadanie 20.
50Zadanie 1.
53Zadanie 2.
53Zadanie 3.
53Zadanie 6.
54Zadanie 7.
54Zadanie 10.
54Ćwiczenie A.
57Zadanie 1.
61Zadanie 2.
61Zadanie 4.
61Zadanie 5.
61Zadanie 7.
62Zadanie 8.
62Zadanie 10.
62Zadanie 11.
62Zadanie 12.
62Zadanie 15.
63Zadanie 17.
63Zadanie 18.
63Zadanie 1.
67Zadanie 2.
67Zadanie 3.
68Zadanie 5.
68Zadanie 12.
69Ćwiczenie A.
70Przykład 2.
73Zadanie 3.
74Zadanie 4.
74Zadanie 5.
75Zadanie 6.
75Zadanie 7.
75Zadanie 8.
75Zadanie 9.
75Zadanie 10.
75Zadanie 11.
76Zadanie 12.
76Zadanie 13.
76Zadanie 15.
77Zadanie 16.
77Zadanie 22.
77Zadanie 23.
78Zadanie 24.
78Zadanie 25.
78Zadanie 1.
81Zadanie 2.
81Zadanie 3.
81Zadanie 4.
81Zadanie 5.
82Zadanie 6.
82Zadanie 7.
82Zadanie 8.
82Zadanie 9.
82Zadanie 10.
83Zadanie 11.
83Zadanie 12.
83Zadanie 1.
84Zadanie 3.
84Zadanie 6.
84Zadanie 7.
84Zadanie 8.
84Zadanie 10.
84
