W tym zadaniu musisz określić, ile powinna wynosić zwycięska stawka w grze, aby gra była sprawiedliwa. Gra polega na losowaniu 3 razy karty z talii 52 kart i oddawaniu wylosowanych kart do talii. Wylosowanie trzech kierów daje szukaną wygraną, wylosowanie 3 pików daje podwójną szukaną wygraną, zaś w innych przypadkach traci się 3 zł.
A – w trzech losowaniach wylosuje się kiery
B – w trzech losowaniach wylosuje się piki
C – pozostałe przypadki, czyli zdarzenie przeciwne do zdarzenia, że wylosuje się trzy kiery lub piki
x – kwota wygranej w przypadku wylosowania trzech kierów
2x – kwota wygranej w przypadku wylosowania trzech pików
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Odp.: Wygrana za wylosowanie trzech kierów powinna wynosić 62 zł, zaś za trzech pików powinna wynosić 124 zł, aby ta gra była sprawiedliwa.

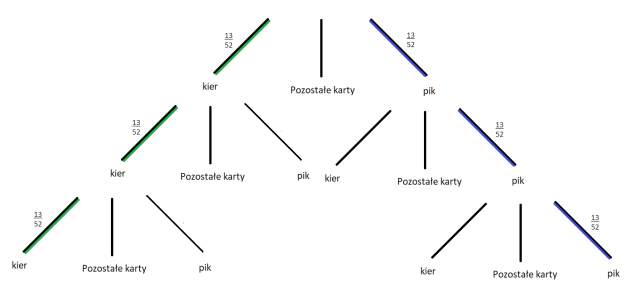
O grze mówimy, że jest sprawiedliwa wtedy, gdy jej wartość oczekiwana wynosi 0. Więc zadanie będzie polegać na przyrównaniu wartości oczekiwanej do 0, podstawieniu za szukaną stawkę x oraz rozwiązanie równania. Jednak, aby uzyskać równanie z x musisz obliczyć prawdopodobieństwa wszystkich zdarzeń. Zauważ, że masz tu do czynienia z doświadczeniem wieloetapowym, więc warto narysować sobie drzewko. Każdy poziom odpowiada kolejnemu losowaniu. Wylosowanie karty innego koloru niż na początku powoduje niespełnienie zwycięskich warunków, więc nie musisz dla tego przypadku rysować dalszych gałęzi. Prawdopodobieństwo wylosowania danej karty obliczasz z klasycznej definicji prawdopodobieństwa dzieląc ilość danych kart przez ilość wszystkich kart. Zauważ, że pozostałe wydarzenia to zdarzenie przeciwne do tego, że wyciągniesz trzy piki lub kiery. Więc aby obliczyć prawdopodobieństwo zdarzenia C wystarczy, że odejmiesz od 1 sumę prawdopodobieństw zdarzeń A i B. Gdy już będziesz miał całe drzewko możesz policzyć szukane prawdopodobieństwa. Mając te wszystkie informacje podstaw je do wzoru na wartość oczekiwaną, przyrównaj to wyrażenie do 0 i oblicz x. Pamiętaj, że stratę zapisuj jako ujemną wygraną. Aby pozbyć się ułamków warto przemnożyć obie strony równania przez wspólny mianownik, czyli 64.

Ćwiczenie A.
43Przykład 1.
43Zadanie 1.
46Zadanie 2.
46Zadanie 4.
46Zadanie 5.
47Zadanie 6.
47Zadanie 7.
47Zadanie 12.
48Zadanie 16.
49Zadanie 18.
49Zadanie 20.
50Zadanie 1.
53Zadanie 2.
53Zadanie 3.
53Zadanie 6.
54Zadanie 7.
54Zadanie 10.
54Ćwiczenie A.
57Zadanie 1.
61Zadanie 2.
61Zadanie 4.
61Zadanie 5.
61Zadanie 7.
62Zadanie 8.
62Zadanie 10.
62Zadanie 11.
62Zadanie 12.
62Zadanie 15.
63Zadanie 17.
63Zadanie 18.
63Zadanie 1.
67Zadanie 2.
67Zadanie 3.
68Zadanie 5.
68Zadanie 12.
69Ćwiczenie A.
70Przykład 2.
73Zadanie 3.
74Zadanie 4.
74Zadanie 5.
75Zadanie 6.
75Zadanie 7.
75Zadanie 8.
75Zadanie 9.
75Zadanie 10.
75Zadanie 11.
76Zadanie 12.
76Zadanie 13.
76Zadanie 15.
77Zadanie 16.
77Zadanie 22.
77Zadanie 23.
78Zadanie 24.
78Zadanie 25.
78Zadanie 1.
81Zadanie 2.
81Zadanie 3.
81Zadanie 4.
81Zadanie 5.
82Zadanie 6.
82Zadanie 7.
82Zadanie 8.
82Zadanie 9.
82Zadanie 10.
83Zadanie 11.
83Zadanie 12.
83Zadanie 1.
84Zadanie 3.
84Zadanie 6.
84Zadanie 7.
84Zadanie 8.
84Zadanie 10.
84
