W tym zadaniu musisz znaleźć wektor, o który należy przesunąć dany okrąg o środku w punkcie S1, aby stykał się zewnętrznie z drugim okręgiem o środku S2 w punkcie (2,–2)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
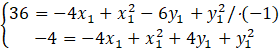
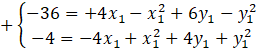
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
O wektor [5,1]

Dane:
Okrąg przed przesunięciem ma środek
![]() i promieniu R = 2
i promieniu R = 2
Okrąg po przesunięciu będzie miał środek
![]() i promieniu R = 2, czyli wiemy, że wektor o początku w punkcie
i promieniu R = 2, czyli wiemy, że wektor o początku w punkcie
![]() i końcu w punkcie P = (2,–2) będzie miał długość 2 (bo R=2). Z tego wynika, że (skorzystaj ze wzoru to
i końcu w punkcie P = (2,–2) będzie miał długość 2 (bo R=2). Z tego wynika, że (skorzystaj ze wzoru to
![]() :
:
Szukamy współrzędnych punktu
![]()
![]()
![]() (skorzystaj ze wzorów skróconego mnożenia)
(skorzystaj ze wzorów skróconego mnożenia)
![]()
![]()
![]() – pierwsze równanie do dalszych obliczeń, bo mamy dwie niewiadome
– pierwsze równanie do dalszych obliczeń, bo mamy dwie niewiadome
![]()
Drugie równanie wyznaczymy z informacji: gdy okręgi będą styczne zewnętrznie w jednym punkcie to suma ich promieniu musi równać się 5 +2 = 7 i będzie to długość wektora łączącego środek okręgu
![]() i
i
![]() . Znowu korzystając ze wzoru na długość wektora obliczamy długość
. Znowu korzystając ze wzoru na długość wektora obliczamy długość
![]() ,
,
![]()
![]()
![]() (skorzystaj ze wzorów skróconego mnożenia)
(skorzystaj ze wzorów skróconego mnożenia)
![]()
![]()
![]() – drugie równanie
– drugie równanie
Zestawiamy układ dwóch równań z dwoma niewiadomymi:
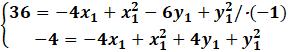
Korzystamy z metody przeciwnych współczynników:
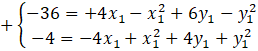
Dodajemy obustronnie oby dwa równania:
![]()
![]()
![]()
Teraz podstawiamy do równania:
![]()
![]()
![]()
Rozwiązujemy równanie kwadratowe obliczając najpierw
![]()
![]()
![]() czyli równanie ma dokładnie jedno rozwiązanie
czyli równanie ma dokładnie jedno rozwiązanie
![]()
![]() czyli wyznaczyliśmy środek współrzędne środka przesuniętego okręgu
czyli wyznaczyliśmy środek współrzędne środka przesuniętego okręgu
![]()
Teraz wyznaczymy współrzędne wektora
![]() odejmując do siebie współrzędne punktów
odejmując do siebie współrzędne punktów
![]()
![]()

Ćwiczenie A.
203Zadanie 1.
205Zadanie 2.
205Zadanie 4.
206Zadanie 6.
206Zadanie 8.
206Zadanie 9.
206Zadanie 10.
207Zadanie 11.
207Zadanie 14.
207Zadanie 15.
207Zadanie 16.
208Zadanie 18.
208Zadanie 20.
208Ćwiczenie D.
211Ćwiczenie E.
211Ćwiczenie G.
212Zadanie 1.
212Zadanie 3.
213Zadanie 4.
213Zadanie 5.
213Zadanie 7.
213Zadanie 8.
213Zadanie 12.
214Ćwiczenie A.
215Zadanie 1.
215Zadanie 2.
216Zadanie 3.
216Zadanie 4.
217Zadanie 5.
217Zadanie 6.
217Zadanie 10.
217Zadanie 11.
217Zadanie 12.
217Zadanie 14.
217Ćwiczenie A.
219Ćwiczenie B.
219Ćwiczenie C.
220Przykład 1.
220Ćwiczenie D.
221Zadanie 1.
222Zadanie 2.
222Zadanie 3.
222Zadanie 4.
223Zadanie 5.
223Zadanie 8.
223Zadanie 9.
224Zadanie 11.
224Zadanie 12.
224Zadanie 13.
224Zadanie 14.
224Zadanie 15.
225Zadanie 16.
225Zadanie 17.
225Zadanie 18.
225Zadanie 19.
225Zadanie 21.
225Ćwiczenie A.
226Ćwiczenie B.
226Przykład 1.
227Zadanie 1.
230Zadanie 2.
230Zadanie 3.
230Zadanie 4.
230Zadanie 6.
230Zadanie 7.
230Zadanie 8.
231Zadanie 9.
231Zadanie 10.
231Zadanie 11.
231Zadanie 12.
231Zadanie 13.
231Zadanie 14.
231Zadanie 15.
232Zadanie 16.
232Zadanie 17.
232Zadanie 18.
232Zadanie 19.
232Zadanie 6
234Zadanie 8.
234Zadanie 9.
234Zadanie 10
234
