W tym zadaniu musisz podać współrzędne wierzchołka W paraboli, która jest wykresem funkcji f, napisać jej wzór funkcji w postaci kanonicznej, napisać równanie osi symetrii wykresu tej funkcji, podać jej zbiór wartości oraz naszkicować wykres i określić liczbę miejsc zerowych funkcji f. Wzór tej funkcji to ![]()
1. ![]()
2. ![]()
3. ![]()
4. ![]()
5. Funkcja ma dwa miejsca zerowe
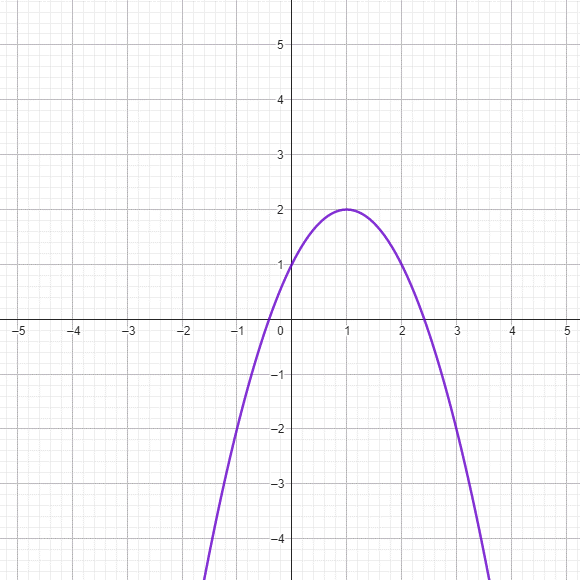

Oblicz współrzędne wierzchołka paraboli, jest nim punkt o współrzędnych (p, q). Skorzystaj ze wzorów i oblicz wartości p i q:![]()
![]()
![]()
![]()
![]()
![]()
Czyli współrzędne wierzchołka paraboli to ![]()
Podstaw obliczone wartości p i q do postaci kanonicznej ![]()
![]()
Osią symetrii paraboli, jest prosta o równaniu ![]()
![]()
Zauważ, że ramiona paraboli są skierowane do dołu, ponieważ współczynnik a jest ujemny, więc zbiorem wartości jest przedział ![]()

Ćwiczenie 3.
255Ćwiczenie 4.
256Ćwiczenie 5.
257Zadanie 12.1.
258Zadanie 12.3.
258Zadanie 12.5.
258Zadanie 12.9.
259Ćwiczenie 7.
260Ćwiczenie 8.
261Ćwiczenie 9.
261Ćwiczenie 10.
261Ćwiczenie 11.
262Ćwiczenie 12.
263Ćwiczenie 13.
263Ćwiczenie 14.
264Zadanie 12.10.
265Zadanie 12.11.
265Zadanie 12.12.
265Zadanie 12.14.
265Zadanie 12.15.
266Zadanie 12.16.
266Zadanie 12.18.
266Ćwiczenie 15.
268Ćwiczenie 16.
268Ćwiczenie 17.
269Zadanie 12.19.
269Zadanie 12.20.
270Zadanie 12.21.
270Zadanie 12.22.
270Ćwiczenie 19.
272Ćwiczenie 20.
274Ćwiczenie 21.
274Zadanie 12.30.
275Zadanie 12.31.
275Zadanie 12.32.
275Zadanie 12.33.
275Zadanie 12.34.
276Zadanie 12.36.
276Ćwiczenie 24.
277Ćwiczenie 25.
279Zadanie 12.38.
279Zadanie 12.39.
279Zadanie 12.40.
280Zadanie 12.44.
280Ćwiczenie 26.
282Ćwiczenie 27.
282Ćwiczenie 28.
283Zadanie 12.46.
283Zadanie 12.47.
284Zadanie 12.48.
284Zadanie 12.49.
284Zadanie 12.50.
284Zadanie 12.51.
284Zadanie 12.53.
285Zadanie 12.54.
285Zadanie 12.55.
285Zadanie 12.56.
285Zadanie 12.57.
286Ćwiczenie 29.
288Ćwiczenie 30.
289Ćwiczenie 32.
290Zadanie 12.58.
291Zadanie 12.59.
291Zadanie 12.60.
291Zadanie 12.61.
291Zadanie 12.62.
291Zadanie 12.63.
291Zadanie 12.65.
292Zadanie 12.71.
292Zadanie 1.
293Zadanie 8.
294Zadanie 9.
294Zadanie 10.
294
