W tym zadaniu musisz za pomocą funkcji zapisać liczbę przekątnych n-kąta i określić jej dziedzinę, a następnie policzyć ile boków ma wielokąt, który ma 405 przekątnych.
![]()
![]()
![]()
![]()
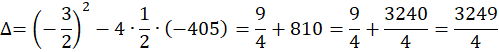
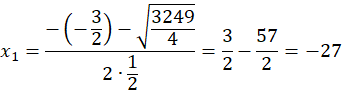
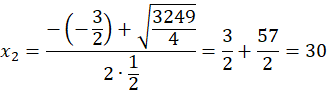
Odpowiedź: Wielokąt o 30 bokach ma 405 przekątnych.

Zauważ, że z każdego boku wychodzi liczba o 3 mniejsza niż ilość kątów, ponieważ przekątna łączy się ze wszystkimi kątami oprócz z tym, z którego wychodzi oraz z kątami sąsiednimi, ale każda przekątna łączy dwa kąty, czyli musisz podzielić przez dwa liczbę przekątnych wychodzących z każdego kąta:![]()
Dziedziną jest zbiór liczb naturalnych, większych od trzech. Oblicz argumenty, dla których funkcja przyjmuje wartość 405:![]()
![]()
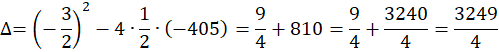
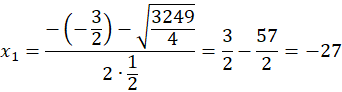
-27 nie należy do dziedziny.
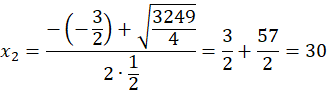
Czyli szukany wielokąt ma 30 boków.

Ćwiczenie 3.
255Ćwiczenie 4.
256Ćwiczenie 5.
257Zadanie 12.1.
258Zadanie 12.3.
258Zadanie 12.5.
258Zadanie 12.9.
259Ćwiczenie 7.
260Ćwiczenie 8.
261Ćwiczenie 9.
261Ćwiczenie 10.
261Ćwiczenie 11.
262Ćwiczenie 12.
263Ćwiczenie 13.
263Ćwiczenie 14.
264Zadanie 12.10.
265Zadanie 12.11.
265Zadanie 12.12.
265Zadanie 12.14.
265Zadanie 12.15.
266Zadanie 12.16.
266Zadanie 12.18.
266Ćwiczenie 15.
268Ćwiczenie 16.
268Ćwiczenie 17.
269Zadanie 12.19.
269Zadanie 12.20.
270Zadanie 12.21.
270Zadanie 12.22.
270Ćwiczenie 19.
272Ćwiczenie 20.
274Ćwiczenie 21.
274Zadanie 12.30.
275Zadanie 12.31.
275Zadanie 12.32.
275Zadanie 12.33.
275Zadanie 12.34.
276Zadanie 12.36.
276Ćwiczenie 24.
277Ćwiczenie 25.
279Zadanie 12.38.
279Zadanie 12.39.
279Zadanie 12.40.
280Zadanie 12.44.
280Ćwiczenie 26.
282Ćwiczenie 27.
282Ćwiczenie 28.
283Zadanie 12.46.
283Zadanie 12.47.
284Zadanie 12.48.
284Zadanie 12.49.
284Zadanie 12.50.
284Zadanie 12.51.
284Zadanie 12.53.
285Zadanie 12.54.
285Zadanie 12.55.
285Zadanie 12.56.
285Zadanie 12.57.
286Ćwiczenie 29.
288Ćwiczenie 30.
289Ćwiczenie 32.
290Zadanie 12.58.
291Zadanie 12.59.
291Zadanie 12.60.
291Zadanie 12.61.
291Zadanie 12.62.
291Zadanie 12.63.
291Zadanie 12.65.
292Zadanie 12.71.
292Zadanie 1.
293Zadanie 8.
294Zadanie 9.
294Zadanie 10.
294
