Dane są proste:
y = 2x + 4
y = -3x – 6
x + 2y – 3 = 0
Wiadomo, że poszczególne punkty ich przecięcia się są wierzchołkami trójkąta. Udowodnij, że jego dwa boki mają tę samą długość, a jeden jego kąt jest kątem prostym. Dodatkowo wyznacz równanie prostej będącą osią symetrii tego wielokąta.
Wprowadź oznaczenia:
k:
y = 2x + 4
l:
y = -3x – 6
m:
x + 2y – 3 = 0
Niech punkt A = (xa, ya) będzie punktem przecięcia się prostych k i l. Wyznacz jego współrzędne:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
A = (-2, 0)
Niech punkt B = (xb, yb) będzie punktem przecięcia się prostych l i m. Wyznacz jego współrzędne:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
B = (-3, 3)
Niech punkt C = (xc, yc) będzie punktem przecięcia się prostych k i m. Wyznacz jego współrzędne:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
C = (-1, 2)
Oblicz długości poszczególnych boków trójkąta ABC:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
W celu wyznaczenia osi symetrii stwórz rysunek poglądowy:
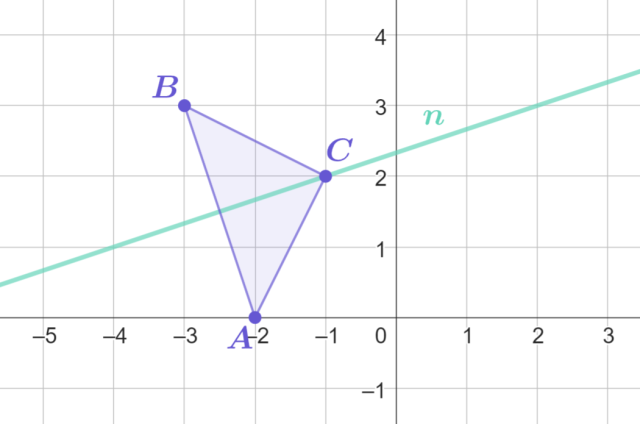
Prosta n jest szukana osią. Jest prostopadła do prostej l: y = -3x – 6 oraz należy do niej punkt C.
n:
![]()
![]()
![]()
![]()
n:
![]()

Wyznacz współrzędne punktów A, B i C powstałych z przecięcia się poszczególnych prostych ze sobą i będących jednocześnie wierzchołkami rozpatrywanego trójkąta.
W celu wyznaczenia ich współrzędnych przyrównaj ze sobą równania poszczególnych prostych.
Następnie wyznacz długości poszczególnych boków i zauważ, że dwa z nich mają taką samą długość, co pokazuje, że trójkąt jest równoramienny. Prostopadłość wykaż, korzystając z twierdzenia odwrotnego do twierdzenia Pitagorasa.
Skonstruuj rysunek trójkąta i narysuj prostą przechodzącą przez wierzchołek leżący przy kącie prostym trójkąta oraz przez środek przeciwprostokątnej. Jest to szukana symetralna.
W celu wyznaczenia jej wzoru zauważ, że jest ona prostopadła do jednej z podanych prostych. Pozwala to wyznaczyć współczynnik kierunkowy (iloczyn współczynników kierunkowych dwóch prostych prostopadłych wynosi -1). Następnie wstaw współrzędne punktu, przez który ona przechodzi i wyznacz jej końcowe równanie.

Ćwiczenie B.
217Ćwiczenie C.
218Zadanie 1.
220Zadanie 2.
220Zadanie 6.
220Zadanie 9.
221Zadanie 12.
221Zadanie 14.
221Zadanie 15.
221Zadanie 17.
221Zadanie 18.
222Zadanie 20.
222Zadanie 21.
222Ćwiczenie A.
223Ćwiczenie B.
224Przykład 2.
226Zadanie 1.
228Zadanie 2.
228Zadanie 4.
228Zadanie 5.
228Zadanie 7.
228Zadanie 8.
228Zadanie 9.
228Zadanie 11.
229Zadanie 12.
229Zadanie 14.
229Zadanie 15.
229Zadanie 16.
229Zadanie 1.
234Zadanie 3.
234Zadanie 4.
234Zadanie 6.
234Zadanie 7.
234Zadanie 8.
234Zadanie 9.
234Zadanie 13.
235Zadanie 15.
235Ćwiczenie B.
236Ćwiczenie C.
237Zadanie 1.
238Zadanie 3.
238Zadanie 4.
239Zadanie 5.
239Zadanie 6.
239Zadanie 8.
239Zadanie 9.
239Zadanie 10.
239Zadanie 11.
239Zadanie 12.
240Zadanie 13.
240Zadanie 1.
245Zadanie 2.
245Zadanie 5.
247Zadanie 6.
247Zadanie 7.
247Zadanie 8.
247Zadanie 11.
247Zadanie 12.
247Zadanie 15.
248Zadanie 16.
248Zadanie 17.
248Zadanie 18.
248Zadanie 1.
250Zadanie 7.
250Zadanie 8.
250
