Dany jest okrąg o równaniu ![]()
Naszkicuj rysunek pomocniczy:
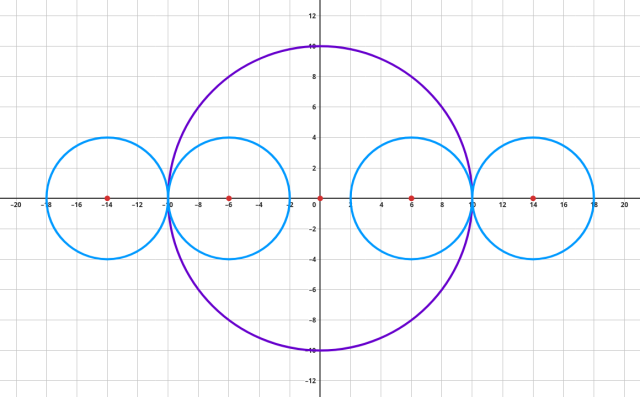
Skoro środki stycznych leżą na osi OX, to ich współrzędne to (𝑎,0). Szukane okręgi mogą być styczne zewnętrznie lub wewnętrznie. Oblicz odległości środków okręgów:
![]()
Sprawdź, dla jakich 𝑥 warunki postawione w treści zadania są spełnione przez okręgi:
![]()
![]()
![]()
![]()
Czyli poszukiwane równania okręgów to:
![]()
![]()
![]()
![]()

Wykorzystaj wzór na długość odcinka:
![]()
by wyznaczyć odległość środków okręgu. Wykorzystaj wzajemne położenie okręgów, żeby wyznaczyć współrzędne środków, dla których okręgi są styczne. Niech 𝑑 będzie odległością środków pewnych okręgów, a 𝑟 i 𝑅 niech będą promieniami tych okręgów. Wzajemne położenia okręgów charakteryzują się następująco:
1. Styczne wewnętrznie: ![]()
2. Styczne zewnętrznie: ![]()
Podstaw obliczone współrzędne środka wraz z promieniem do wzoru:
![]()
gdzie ![]()

Ćwiczenie B.
217Ćwiczenie C.
218Zadanie 1.
220Zadanie 2.
220Zadanie 6.
220Zadanie 9.
221Zadanie 12.
221Zadanie 14.
221Zadanie 15.
221Zadanie 17.
221Zadanie 18.
222Zadanie 20.
222Zadanie 21.
222Ćwiczenie A.
223Ćwiczenie B.
224Przykład 2.
226Zadanie 1.
228Zadanie 2.
228Zadanie 4.
228Zadanie 5.
228Zadanie 7.
228Zadanie 8.
228Zadanie 9.
228Zadanie 11.
229Zadanie 12.
229Zadanie 14.
229Zadanie 15.
229Zadanie 16.
229Zadanie 1.
234Zadanie 3.
234Zadanie 4.
234Zadanie 6.
234Zadanie 7.
234Zadanie 8.
234Zadanie 9.
234Zadanie 13.
235Zadanie 15.
235Ćwiczenie B.
236Ćwiczenie C.
237Zadanie 1.
238Zadanie 3.
238Zadanie 4.
239Zadanie 5.
239Zadanie 6.
239Zadanie 8.
239Zadanie 9.
239Zadanie 10.
239Zadanie 11.
239Zadanie 12.
240Zadanie 13.
240Zadanie 1.
245Zadanie 2.
245Zadanie 5.
247Zadanie 6.
247Zadanie 7.
247Zadanie 8.
247Zadanie 11.
247Zadanie 12.
247Zadanie 15.
248Zadanie 16.
248Zadanie 17.
248Zadanie 18.
248Zadanie 1.
250Zadanie 7.
250Zadanie 8.
250
