Dany jest trójkąt prostokątny wpisany w okrąg: x² + y² – 6x + 4y = 0. Jego boki tworzą pewne trzy proste. Wyznacz je, wiedząc, że jedna z nich (zawierająca jedną z przyprostokątnych) ma równanie: x + 5y – 6 = 0.

Wprowadź oznaczenia:

Szukane są równania prostych l i m.

S = (3, -2)

$\text{[math]}$

x + 5y – 6 = 0

x = -5y + 6

Rozpatrz dwa przypadki:

Pierwszy przypadek – przeciwprostokątną jest odcinek BC:

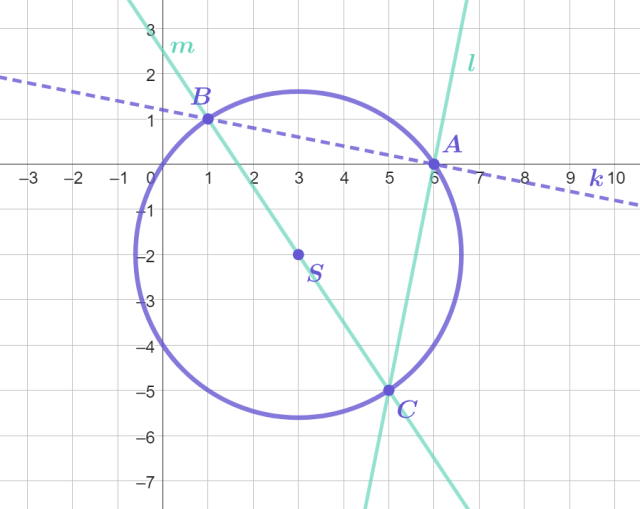
Aby znaleźć współrzędne punktów A i B przyrównaj ze sobą równanie prostej k oraz równanie okręgu:

$\text{[math]}$

A = (0, 6), B = (1, 1)

Zapisz równanie prostej m jako:

$\text{[math]}$

Do prostej tej należą punkty B i S. Ułóż zatem układ równań:

$\text{[math]}$

Punkt C należy do tej prostej, zapisz zatem jego współrzędne w postaci:

$\text{[math]}$

Długość odcinka |BC| jest równa długości dwóch promieni okręgu, co wynika z własności trójkąta prostokątnego wpisanego w okrąg. Zatem:

$\text{[math]}$

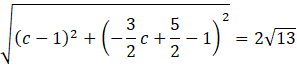
Obie strony równania są nieujemne, można je zatem podnieść obustronnie do kwadratu:

$\text{[math]}$

Warunki zadania spełnia liczba $\text{[math]}$ , zatem:

$\text{[math]}$

Zapisz równanie prostej l jako:

$\text{[math]}$

Do prostej tej należą punkty A i C. Ułóż zatem układ równań:

$\text{[math]}$

Drugi przypadek – przeciwprostokątną jest odcinek AC:

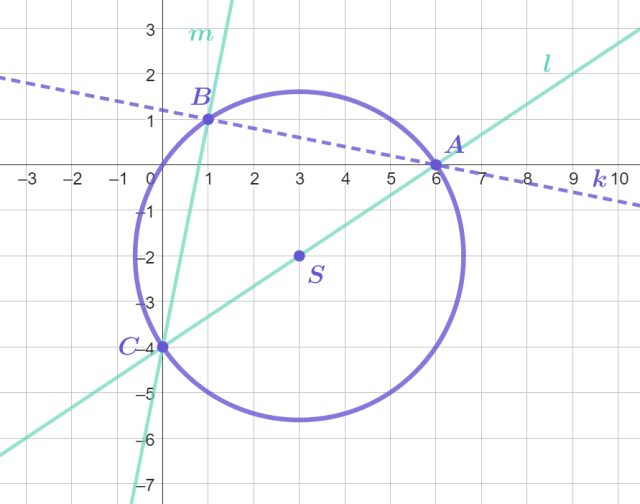
Współrzędne punktów A i B pozostają takie same jak w przypadku pierwszym i mają postać:

A = (0, 6), B = (1, 1)

Zapisz równanie prostej l jako:

$\text{[math]}$

Do prostej tej należą punkty A i S. Ułóż zatem układ równań:

$\text{[math]}$

Punkt C należy do tej prostej, zapisz zatem jego współrzędne w postaci:

$\text{[math]}$

Długość odcinka |AC| jest równa długości dwóch promieni okręgu, co wynika z własności trójkąta prostokątnego wpisanego w okrąg. Zatem:

$\text{[math]}$

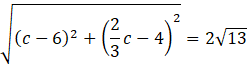
Obie strony równania są nieujemne, można je zatem podnieść obustronnie do kwadratu:

$\text{[math]}$

Warunki zadania spełnia liczba $\text{[math]}$ , zatem:

$\text{[math]}$

Zapisz równanie prostej m jako:

$\text{[math]}$

Do prostej tej należą punkty B i C. Ułóż zatem układ równań:

$\text{[math]}$

Końcowa odpowiedź:

3x + 2y – 5 = 0 oraz 5x – y – 30 = 0

lub

2x – 3y – 12 = 0 oraz 5x – y – 4 = 0

Stwórz rysunek pomocniczy i wprowadź odpowiednie oznaczenia. Rozpatrz dwa przypadki: w zależności od tego, który bok trójkąta jest jego przeciwprostokątną. W każdym z tych przypadków:

Znajdź współrzędne dwóch wierzchołków trójkąta, które należą do prostej podanej w treści zadania. W tym celu przyrównaj równanie prostej i równanie okręgu, a następnie rozwiąż otrzymany w ten sposób układ.

Zauważ, że środek okręgu oraz jeden z wyznaczonych punków należą do jednej z szukanych prostych. Wyznacz jej równanie, wstawiając do równania w postaci y = ax + b ich współrzędne i rozwiązując powstały układ.

Zwróć uwagę, że do wyznaczonej prostej należy trzeci wierzchołek trójkąta. Wyznacz dzięki temu jego przykładowe współrzędne. Następnie skorzystaj z zależności, że przeciwprostokątna w trójkącie opisanym na okręgu jest równa średnicy tego okręgu. Na podstawie tej informacji ułóż odpowiednie równanie i wyznacz współrzędne trzeciego wierzchołka trójkąta.

Wyznacz równanie drugiej z szukanych prostych, wstawiając do równania w postaci y = ax + b współrzędne dwóch punktów, które do tej prostej należą.