Dany jest okrąg ![]()
![]()
Naszkicuj rysunek pomocniczy:
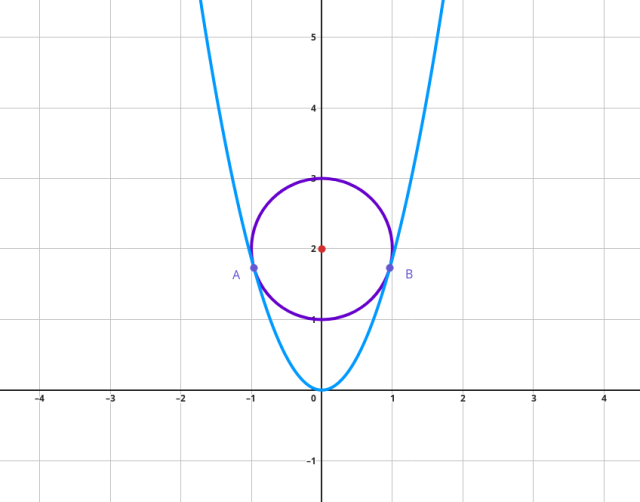
Ułóż układ równań:
![]()
Podstaw równanie paraboli do równania okręgu:
![]()
![]()
![]()
Otrzymane równanie to równanie dwukwadratowe. Podstaw ![]()
![]()
![]()
Oblicz wyróżnik wielomianu stopnia drugiego:
![]()
![]()
![]()
Masz do czynienia z równaniem dwukwadratowym „w ukryciu”. Dla każdego pojedynczego rozwiązania zmiennej 𝑡 otrzymasz dwa rozwiązania zmiennej 𝑥. Punktów przecięcia ma być dokładnie dwa, więc należy przyrównać otrzymany wyróżnik do zera:
![]()
![]()
![]()
![]()
![]()
Dla tych wartości parametru 𝑚 wielomian o zmiennej 𝑡 ma dokładnie jedno rozwiązanie, czyli:
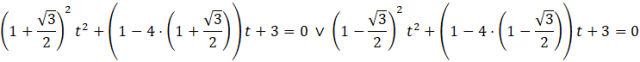
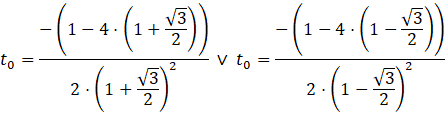
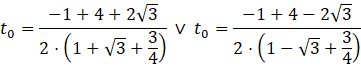
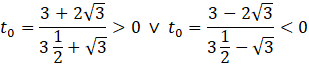
Dla ![]()
Odp. ![]()

Ułóż układ równań z równania okręgu oraz paraboli. Wstaw równanie paraboli do równania okręgu. Wykonaj zamianę zmiennej ![]()
![]()
![]()
a pierwiastek z trzech ma wartość w przybliżeniu 1,73.

Ćwiczenie B.
217Ćwiczenie C.
218Zadanie 1.
220Zadanie 2.
220Zadanie 6.
220Zadanie 9.
221Zadanie 12.
221Zadanie 14.
221Zadanie 15.
221Zadanie 17.
221Zadanie 18.
222Zadanie 20.
222Zadanie 21.
222Ćwiczenie A.
223Ćwiczenie B.
224Przykład 2.
226Zadanie 1.
228Zadanie 2.
228Zadanie 4.
228Zadanie 5.
228Zadanie 7.
228Zadanie 8.
228Zadanie 9.
228Zadanie 11.
229Zadanie 12.
229Zadanie 14.
229Zadanie 15.
229Zadanie 16.
229Zadanie 1.
234Zadanie 3.
234Zadanie 4.
234Zadanie 6.
234Zadanie 7.
234Zadanie 8.
234Zadanie 9.
234Zadanie 13.
235Zadanie 15.
235Ćwiczenie B.
236Ćwiczenie C.
237Zadanie 1.
238Zadanie 3.
238Zadanie 4.
239Zadanie 5.
239Zadanie 6.
239Zadanie 8.
239Zadanie 9.
239Zadanie 10.
239Zadanie 11.
239Zadanie 12.
240Zadanie 13.
240Zadanie 1.
245Zadanie 2.
245Zadanie 5.
247Zadanie 6.
247Zadanie 7.
247Zadanie 8.
247Zadanie 11.
247Zadanie 12.
247Zadanie 15.
248Zadanie 16.
248Zadanie 17.
248Zadanie 18.
248Zadanie 1.
250Zadanie 7.
250Zadanie 8.
250
