Wyznacz długość promienia okręgu ze środkiem w punkcie S, którego cięciwa, o długości 4, zawiera się w podanej prostej.
Zauważ, że promienie okręgu S, które przecinają się z podaną prostą, tworzą trójkąt równoramienny o podstawie równej długości cięciwy.
Przekształć równanie podanej prostej na postać ogólną:
![]()
![]()
![]()
Wykorzystaj wzór na obliczenie odległości pomiędzy prostą a punktem, aby obliczyć odległość punktu S od cięciwy:
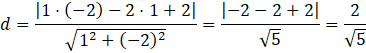
Pozbądź się niewymierności z mianownika:
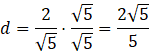
Zauważ, że podana odległość, połowa cięciwy oraz promień tworzą trójkąt prostokątny, którego przeciwprostokątną jest promień. Wykorzystaj twierdzenie Pitagorasa do obliczenia długości promienia:
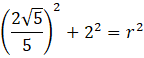
![]()
![]()
![]()
![]()
Promień nie może być ujemny, a więc:
![]()

Zauważ, że promienie okręgu S, które przecinają się z podaną prostą, tworzą trójkąt równoramienny o podstawie równej długości cięciwy. Możesz opuścić wysokość tego trójkąta z wierzchołka S i wtedy będziesz w stanie obliczyć promień z twierdzenia Pitagorasa. Promień będzie wtedy przeciwprostokątną tego trójkąta.
Najpierw przekształć podane równanie z postaci kierunkowej ![]()
![]()
![]()
![]()
![]()

Ćwiczenie B.
217Ćwiczenie C.
218Zadanie 1.
220Zadanie 2.
220Zadanie 6.
220Zadanie 9.
221Zadanie 12.
221Zadanie 14.
221Zadanie 15.
221Zadanie 17.
221Zadanie 18.
222Zadanie 20.
222Zadanie 21.
222Ćwiczenie A.
223Ćwiczenie B.
224Przykład 2.
226Zadanie 1.
228Zadanie 2.
228Zadanie 4.
228Zadanie 5.
228Zadanie 7.
228Zadanie 8.
228Zadanie 9.
228Zadanie 11.
229Zadanie 12.
229Zadanie 14.
229Zadanie 15.
229Zadanie 16.
229Zadanie 1.
234Zadanie 3.
234Zadanie 4.
234Zadanie 6.
234Zadanie 7.
234Zadanie 8.
234Zadanie 9.
234Zadanie 13.
235Zadanie 15.
235Ćwiczenie B.
236Ćwiczenie C.
237Zadanie 1.
238Zadanie 3.
238Zadanie 4.
239Zadanie 5.
239Zadanie 6.
239Zadanie 8.
239Zadanie 9.
239Zadanie 10.
239Zadanie 11.
239Zadanie 12.
240Zadanie 13.
240Zadanie 1.
245Zadanie 2.
245Zadanie 5.
247Zadanie 6.
247Zadanie 7.
247Zadanie 8.
247Zadanie 11.
247Zadanie 12.
247Zadanie 15.
248Zadanie 16.
248Zadanie 17.
248Zadanie 18.
248Zadanie 1.
250Zadanie 7.
250Zadanie 8.
250
