Dany jest okrąg ![]()
![]()
Naszkicuj rysunek pomocniczy:
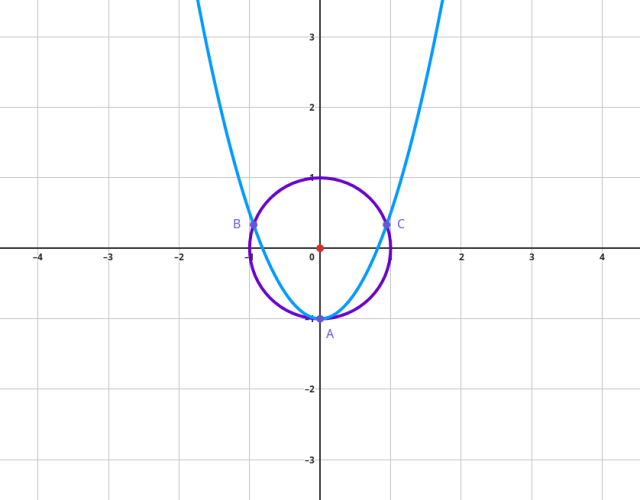
Ułóż układ równań:
![]()
Podstaw równanie paraboli do równania okręgu:
![]()
![]()
![]()
![]()
Czyli:
![]()
![]()
![]()
![]()
Wyróżnik musi być większy od zera, by wyrażenie miało dwa miejsca zerowe:
![]()
Odczytaj miejsca zerowe wyróżnika, a następnie naszkicuj wykres funkcji:
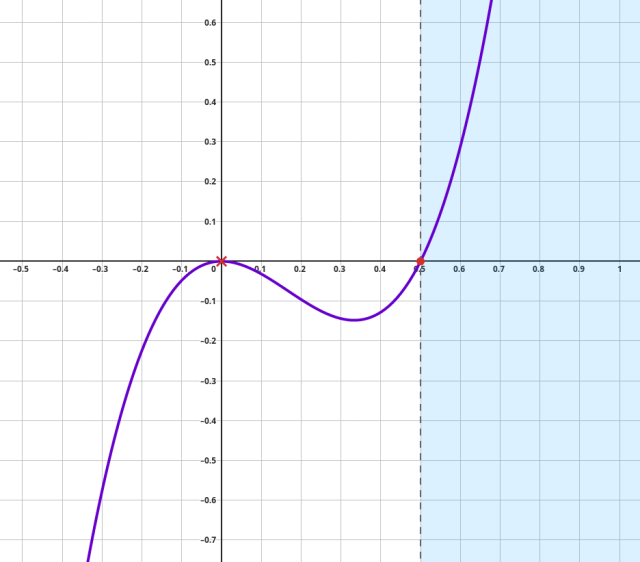
Czyli wyróżnik jest większy od zera dla ![]()
Odp. ![]()

Ułóż układ równań z równania okręgu oraz paraboli. Wstaw równanie paraboli do równania okręgu. Wylicz wyróżnik nowo powstałego wielomianu. Zauważ, że bez względu na 𝑚, okrąg i parabola zawsze będą miały jedno rozwiązanie – 𝑥 = 0. Oblicz wyróżnik drugiego wyrażenia i sprawdź, dla jakich wartości 𝑚 jest on większy od zera (dwa punkty wspólne). Naszkicuj wykres wielomianu trzeciego stopnia i odczytaj odpowiedni przedział.

Ćwiczenie B.
217Ćwiczenie C.
218Zadanie 1.
220Zadanie 2.
220Zadanie 6.
220Zadanie 9.
221Zadanie 12.
221Zadanie 14.
221Zadanie 15.
221Zadanie 17.
221Zadanie 18.
222Zadanie 20.
222Zadanie 21.
222Ćwiczenie A.
223Ćwiczenie B.
224Przykład 2.
226Zadanie 1.
228Zadanie 2.
228Zadanie 4.
228Zadanie 5.
228Zadanie 7.
228Zadanie 8.
228Zadanie 9.
228Zadanie 11.
229Zadanie 12.
229Zadanie 14.
229Zadanie 15.
229Zadanie 16.
229Zadanie 1.
234Zadanie 3.
234Zadanie 4.
234Zadanie 6.
234Zadanie 7.
234Zadanie 8.
234Zadanie 9.
234Zadanie 13.
235Zadanie 15.
235Ćwiczenie B.
236Ćwiczenie C.
237Zadanie 1.
238Zadanie 3.
238Zadanie 4.
239Zadanie 5.
239Zadanie 6.
239Zadanie 8.
239Zadanie 9.
239Zadanie 10.
239Zadanie 11.
239Zadanie 12.
240Zadanie 13.
240Zadanie 1.
245Zadanie 2.
245Zadanie 5.
247Zadanie 6.
247Zadanie 7.
247Zadanie 8.
247Zadanie 11.
247Zadanie 12.
247Zadanie 15.
248Zadanie 16.
248Zadanie 17.
248Zadanie 18.
248Zadanie 1.
250Zadanie 7.
250Zadanie 8.
250
