Wiedząc, że Q = (x, 2x), P = (1, -2), R = (4, -3) oraz trójkąt PQR jest równoramienny, wyznacz Q.
Pierwszy przypadek, gdy odcinek PR jest podstawą trójkąta.
Wiesz, że |PQ|=|RQ|, więc wykorzystaj wzór na długość odcinka w układzie współrzędnych i rozwiąż równanie:
![]()
![]()
![]()
Uprość równanie:
![]()
![]()
Współrzędne Q to (10, 20).
Drugi przypadek, gdy odcinek PR jest ramieniem trójkąta.
Wiesz, że |PR|=|PQ|, więc wykorzystaj wzór na długość odcinka w układzie współrzędnych, oblicz długość PR:
![]()
Oblicz |PQ|:
![]()
![]()
![]()
Uprość równanie:
![]()
Rozwiąż równanie kwadratowe, obliczając deltę:
![]()
![]()
![]()
![]()
Współrzędne wierzchołka Q to:
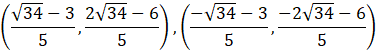

Zauważ, że są dwa możliwe przypadki, w jednym z nich bok PR jest podstawą trójkąta, a w drugim – ramieniem. Wykorzystując wzór na odległość między punktami w układzie współrzędnych![]()

Ćwiczenie B.
217Ćwiczenie C.
218Zadanie 1.
220Zadanie 2.
220Zadanie 6.
220Zadanie 9.
221Zadanie 12.
221Zadanie 14.
221Zadanie 15.
221Zadanie 17.
221Zadanie 18.
222Zadanie 20.
222Zadanie 21.
222Ćwiczenie A.
223Ćwiczenie B.
224Przykład 2.
226Zadanie 1.
228Zadanie 2.
228Zadanie 4.
228Zadanie 5.
228Zadanie 7.
228Zadanie 8.
228Zadanie 9.
228Zadanie 11.
229Zadanie 12.
229Zadanie 14.
229Zadanie 15.
229Zadanie 16.
229Zadanie 1.
234Zadanie 3.
234Zadanie 4.
234Zadanie 6.
234Zadanie 7.
234Zadanie 8.
234Zadanie 9.
234Zadanie 13.
235Zadanie 15.
235Ćwiczenie B.
236Ćwiczenie C.
237Zadanie 1.
238Zadanie 3.
238Zadanie 4.
239Zadanie 5.
239Zadanie 6.
239Zadanie 8.
239Zadanie 9.
239Zadanie 10.
239Zadanie 11.
239Zadanie 12.
240Zadanie 13.
240Zadanie 1.
245Zadanie 2.
245Zadanie 5.
247Zadanie 6.
247Zadanie 7.
247Zadanie 8.
247Zadanie 11.
247Zadanie 12.
247Zadanie 15.
248Zadanie 16.
248Zadanie 17.
248Zadanie 18.
248Zadanie 1.
250Zadanie 7.
250Zadanie 8.
250
