Dane są dwa okręgi: pierwszy, o równaniu ![]()
![]()
Naszkicuj rysunek pomocniczy:
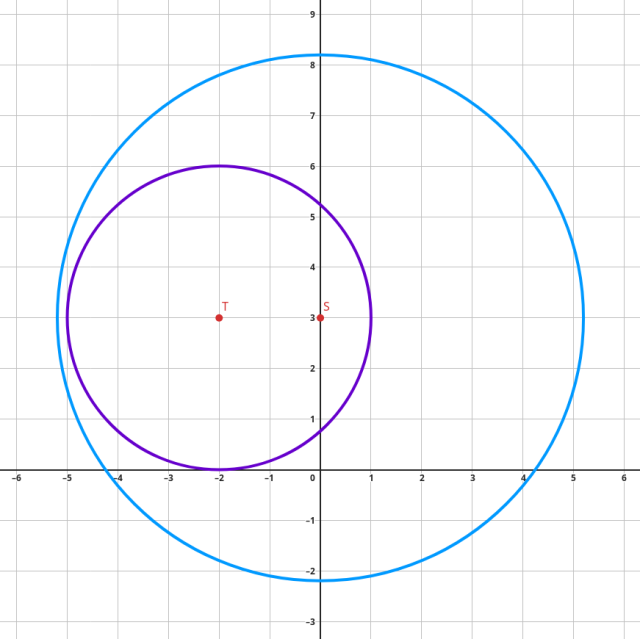
Z rysunku zauważ, że okręgi nie powinny mieć punktów wspólnych. Potwierdź to za pomocą obliczeń.
Ułóż i rozwiąż układ równań:
![]()
![]()
![]()
Odejmij równania stronami:
![]()
![]()
Podstaw otrzymane równanie prostej do jednego z równań okręgu:
![]()
![]()
![]()
Nie istnieją rozwiązania tego równania w zbiorze liczb rzeczywistych. Okręgi nie mają wspólnych punktów.

Ułóż układ równań z równań okręgów. Przeprowadź te równania do postaci ogólnej, a następnie dodaj stronami. Podstaw otrzymaną w ten sposób prostą do jednego z równań okręgów. W wyniku otrzymasz, że kwadrat liczby zależnej od 𝑦 jest równy liczbie ujemnej. Równanie nie ma żadnych rozwiązań; okręgi się nie przecinają. Równoważnie można pokazać, że okręgi są rozłączne wewnętrznie.

Ćwiczenie B.
217Ćwiczenie C.
218Zadanie 1.
220Zadanie 2.
220Zadanie 6.
220Zadanie 9.
221Zadanie 12.
221Zadanie 14.
221Zadanie 15.
221Zadanie 17.
221Zadanie 18.
222Zadanie 20.
222Zadanie 21.
222Ćwiczenie A.
223Ćwiczenie B.
224Przykład 2.
226Zadanie 1.
228Zadanie 2.
228Zadanie 4.
228Zadanie 5.
228Zadanie 7.
228Zadanie 8.
228Zadanie 9.
228Zadanie 11.
229Zadanie 12.
229Zadanie 14.
229Zadanie 15.
229Zadanie 16.
229Zadanie 1.
234Zadanie 3.
234Zadanie 4.
234Zadanie 6.
234Zadanie 7.
234Zadanie 8.
234Zadanie 9.
234Zadanie 13.
235Zadanie 15.
235Ćwiczenie B.
236Ćwiczenie C.
237Zadanie 1.
238Zadanie 3.
238Zadanie 4.
239Zadanie 5.
239Zadanie 6.
239Zadanie 8.
239Zadanie 9.
239Zadanie 10.
239Zadanie 11.
239Zadanie 12.
240Zadanie 13.
240Zadanie 1.
245Zadanie 2.
245Zadanie 5.
247Zadanie 6.
247Zadanie 7.
247Zadanie 8.
247Zadanie 11.
247Zadanie 12.
247Zadanie 15.
248Zadanie 16.
248Zadanie 17.
248Zadanie 18.
248Zadanie 1.
250Zadanie 7.
250Zadanie 8.
250
