Dane są dwa okręgi: o środku w ![]()
![]()
Wzory kanoniczne tych okręgów to:
![]()
![]()
Naszkicuj rysunek pomocniczy:
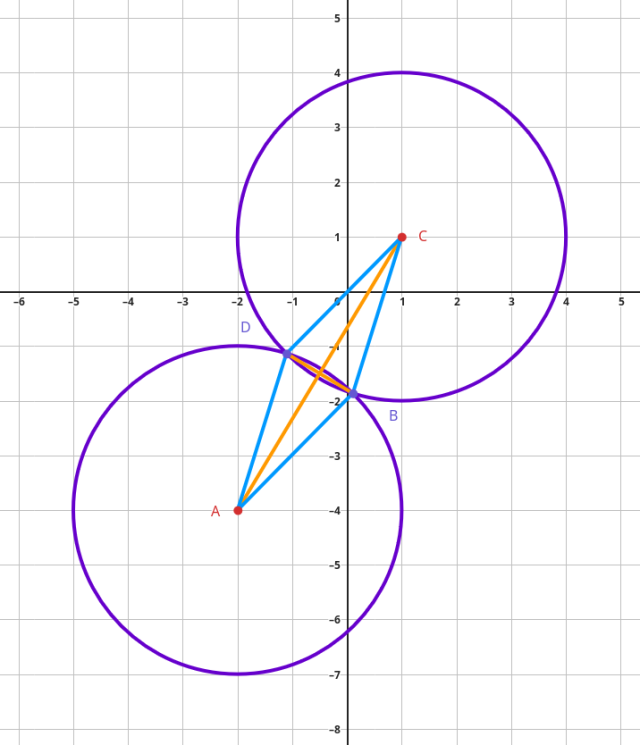
Zauważ, że boki czworokąta to promienie okręgów o długości 3. Czworokąt 𝐴𝐵𝐶𝐷 jest więc rombem.
Oblicz długość odcinka 𝐴𝐶:
![]()
Oblicz cosinus kąta 𝐴𝐵𝐶 za pomocą twierdzenia cosinusów:
![]()
![]()
![]()
![]()
Oblicz sinus kąta 𝐴𝐵𝐶, wykorzystując jedynkę trygonometryczną:
![]()
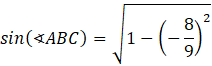
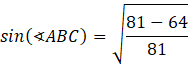
![]()
Oblicz pole rombu:
![]()

Naszkicuj okręgi z treści zadania oraz czworokąt 𝐴𝐵𝐶𝐷. Zauważ, że ta figura jest rombem. Oblicz długość dłuższej przekątnej, łączącej ze sobą środki okręgów. Za pomocą twierdzenia cosinusów oraz jedynki trygonometrycznej wyznacz sinus kąta między ramionami czworokąta. Skorzystaj ze wzoru na pole rombu:
![]()

Ćwiczenie B.
217Ćwiczenie C.
218Zadanie 1.
220Zadanie 2.
220Zadanie 6.
220Zadanie 9.
221Zadanie 12.
221Zadanie 14.
221Zadanie 15.
221Zadanie 17.
221Zadanie 18.
222Zadanie 20.
222Zadanie 21.
222Ćwiczenie A.
223Ćwiczenie B.
224Przykład 2.
226Zadanie 1.
228Zadanie 2.
228Zadanie 4.
228Zadanie 5.
228Zadanie 7.
228Zadanie 8.
228Zadanie 9.
228Zadanie 11.
229Zadanie 12.
229Zadanie 14.
229Zadanie 15.
229Zadanie 16.
229Zadanie 1.
234Zadanie 3.
234Zadanie 4.
234Zadanie 6.
234Zadanie 7.
234Zadanie 8.
234Zadanie 9.
234Zadanie 13.
235Zadanie 15.
235Ćwiczenie B.
236Ćwiczenie C.
237Zadanie 1.
238Zadanie 3.
238Zadanie 4.
239Zadanie 5.
239Zadanie 6.
239Zadanie 8.
239Zadanie 9.
239Zadanie 10.
239Zadanie 11.
239Zadanie 12.
240Zadanie 13.
240Zadanie 1.
245Zadanie 2.
245Zadanie 5.
247Zadanie 6.
247Zadanie 7.
247Zadanie 8.
247Zadanie 11.
247Zadanie 12.
247Zadanie 15.
248Zadanie 16.
248Zadanie 17.
248Zadanie 18.
248Zadanie 1.
250Zadanie 7.
250Zadanie 8.
250
