Dany jest punkt P należący do prostej y = 2x + 10. Wyznacz go, wiedząc, że ze wszystkich punktów leżących na podanej prostej, odległość punktu P od punktu (0, 0) jest najmniejsza.
Współrzędne punktu P można zapisać jako:
![]()
Oznacz prostą y = 2x + 10 jako k, oraz punkt S = (0, 0)
k:
2x – y + 10 = 0
Z informacji z treści zadania wynika, że odległość punktu S od prostej k jest równa długości odcinka PS. Zapisz tę zależność równaniem:
![]()
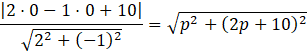
![]()
![]()
Obie strony równania są nieujemne, można je zatem obustronnie podnieść do kwadratu:
![]()
![]()
![]()
![]()
![]()
![]()
Odpowiedź:
P = (-4, 2)

Wiedząc, że punkt należy do prostej, której równanie kierunkowe zostało podane, wyznacz jego współrzędne przy pomocy jednej niewiadomej.
Przeanalizuj informacje z treści zadania i wywnioskuj, że odległość punktu (0, 0) od prostej podanej w treści zadania, jest równa długości odcinka tworzonego przez punkty P i punkt (0, 0).
Przyrównaj ze sobą te wielkości za pomocą odpowiedniego równania. Rozwiąż je i wyznacz współrzędne punktu P.

Ćwiczenie B.
217Ćwiczenie C.
218Zadanie 1.
220Zadanie 2.
220Zadanie 6.
220Zadanie 9.
221Zadanie 12.
221Zadanie 14.
221Zadanie 15.
221Zadanie 17.
221Zadanie 18.
222Zadanie 20.
222Zadanie 21.
222Ćwiczenie A.
223Ćwiczenie B.
224Przykład 2.
226Zadanie 1.
228Zadanie 2.
228Zadanie 4.
228Zadanie 5.
228Zadanie 7.
228Zadanie 8.
228Zadanie 9.
228Zadanie 11.
229Zadanie 12.
229Zadanie 14.
229Zadanie 15.
229Zadanie 16.
229Zadanie 1.
234Zadanie 3.
234Zadanie 4.
234Zadanie 6.
234Zadanie 7.
234Zadanie 8.
234Zadanie 9.
234Zadanie 13.
235Zadanie 15.
235Ćwiczenie B.
236Ćwiczenie C.
237Zadanie 1.
238Zadanie 3.
238Zadanie 4.
239Zadanie 5.
239Zadanie 6.
239Zadanie 8.
239Zadanie 9.
239Zadanie 10.
239Zadanie 11.
239Zadanie 12.
240Zadanie 13.
240Zadanie 1.
245Zadanie 2.
245Zadanie 5.
247Zadanie 6.
247Zadanie 7.
247Zadanie 8.
247Zadanie 11.
247Zadanie 12.
247Zadanie 15.
248Zadanie 16.
248Zadanie 17.
248Zadanie 18.
248Zadanie 1.
250Zadanie 7.
250Zadanie 8.
250
