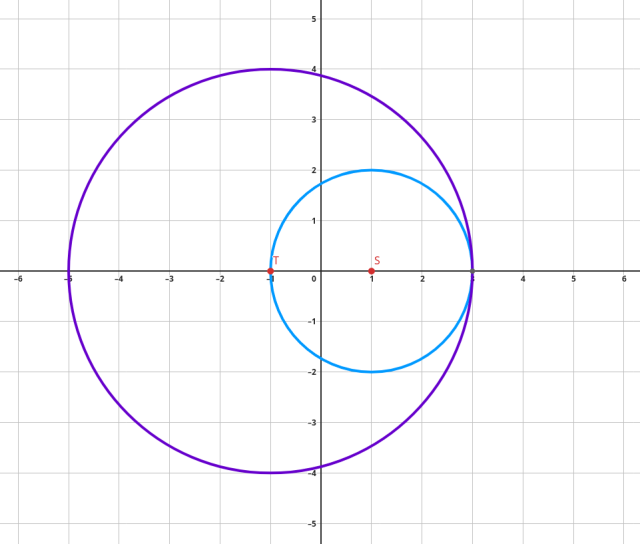
Dane są dwa okręgi: pierwszy, o środku w 𝑆=(1,0) i promieniu 2 oraz drugi, o środku w 𝑇=(-1,0) i promieniu 4. Wyznacz współrzędne punktów przecięcia tych dwóch okręgów.
Wykorzystaj wzór na okrąg o danym środku i promieniu, by wyznaczyć równania okręgów z zadania:
![]()
![]()
Naszkicuj rysunek pomocniczy:
Ułóż i rozwiąż układ równań:
![]()
![]()
Odejmij równania stronami:
![]()
![]()
Podstaw otrzymane równanie prostej do jednego z równań okręgu:
![]()
![]()
![]()
Odp. ![]()

Wyznacz za pomocą wzoru na okrąg równania okręgów podanych w zdaniu:
![]()
gdzie (𝑎,𝑏) to współrzędne środka okręgu, a 𝑟 to jego promień.
Ułóż układ równań z równań okręgów. Przeprowadź te równania do postaci ogólnej, a następnie dodaj stronami. Podstaw otrzymaną w ten sposób prostą do jednego z równań okręgów. Otrzymane wartości to współrzędne punktów przecięcia na osi rzędnych.

Ćwiczenie B.
217Ćwiczenie C.
218Zadanie 1.
220Zadanie 2.
220Zadanie 6.
220Zadanie 9.
221Zadanie 12.
221Zadanie 14.
221Zadanie 15.
221Zadanie 17.
221Zadanie 18.
222Zadanie 20.
222Zadanie 21.
222Ćwiczenie A.
223Ćwiczenie B.
224Przykład 2.
226Zadanie 1.
228Zadanie 2.
228Zadanie 4.
228Zadanie 5.
228Zadanie 7.
228Zadanie 8.
228Zadanie 9.
228Zadanie 11.
229Zadanie 12.
229Zadanie 14.
229Zadanie 15.
229Zadanie 16.
229Zadanie 1.
234Zadanie 3.
234Zadanie 4.
234Zadanie 6.
234Zadanie 7.
234Zadanie 8.
234Zadanie 9.
234Zadanie 13.
235Zadanie 15.
235Ćwiczenie B.
236Ćwiczenie C.
237Zadanie 1.
238Zadanie 3.
238Zadanie 4.
239Zadanie 5.
239Zadanie 6.
239Zadanie 8.
239Zadanie 9.
239Zadanie 10.
239Zadanie 11.
239Zadanie 12.
240Zadanie 13.
240Zadanie 1.
245Zadanie 2.
245Zadanie 5.
247Zadanie 6.
247Zadanie 7.
247Zadanie 8.
247Zadanie 11.
247Zadanie 12.
247Zadanie 15.
248Zadanie 16.
248Zadanie 17.
248Zadanie 18.
248Zadanie 1.
250Zadanie 7.
250Zadanie 8.
250
