Dany jest układ równań sparametryzowany względem 𝑝. Znajdź takie 𝑝, że układ równań:
![]()
jest sprzeczny.
Zinterpretuj równania w układzie równań jako proste. Przekształć wzory ogólne do postaci kierunkowej:
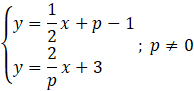
Dla 𝑝 = 0:
![]()
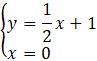
Proste nie są równoległe, czyli 𝑝 = 0 nie spełnia warunków zadania.
Proste są równoległe i nie mają punktów wspólnych, gdy współczynniki kierunkowe są równe, a wyrazy wolne są różne:

![]()
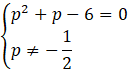
Nie istnieje 𝑝 spełniające te warunki; układ równań nigdy nie jest sprzeczny.

Przekształć równania do postaci kierunkowej prostej. Interpretując równania jako proste w układzie współrzędnych, a rozwiązania jako punkty przecięcia, ustaw współczynniki kierunkowe i wyrazy wolne tak, aby proste nie miały punktów wspólnych.

Ćwiczenie B.
217Ćwiczenie C.
218Zadanie 1.
220Zadanie 2.
220Zadanie 6.
220Zadanie 9.
221Zadanie 12.
221Zadanie 14.
221Zadanie 15.
221Zadanie 17.
221Zadanie 18.
222Zadanie 20.
222Zadanie 21.
222Ćwiczenie A.
223Ćwiczenie B.
224Przykład 2.
226Zadanie 1.
228Zadanie 2.
228Zadanie 4.
228Zadanie 5.
228Zadanie 7.
228Zadanie 8.
228Zadanie 9.
228Zadanie 11.
229Zadanie 12.
229Zadanie 14.
229Zadanie 15.
229Zadanie 16.
229Zadanie 1.
234Zadanie 3.
234Zadanie 4.
234Zadanie 6.
234Zadanie 7.
234Zadanie 8.
234Zadanie 9.
234Zadanie 13.
235Zadanie 15.
235Ćwiczenie B.
236Ćwiczenie C.
237Zadanie 1.
238Zadanie 3.
238Zadanie 4.
239Zadanie 5.
239Zadanie 6.
239Zadanie 8.
239Zadanie 9.
239Zadanie 10.
239Zadanie 11.
239Zadanie 12.
240Zadanie 13.
240Zadanie 1.
245Zadanie 2.
245Zadanie 5.
247Zadanie 6.
247Zadanie 7.
247Zadanie 8.
247Zadanie 11.
247Zadanie 12.
247Zadanie 15.
248Zadanie 16.
248Zadanie 17.
248Zadanie 18.
248Zadanie 1.
250Zadanie 7.
250Zadanie 8.
250
