Mając dane równanie prostej ![]()
![]()
Jeśli proste mają być równoległe do podanej prostej, to muszą mieć taki sam współczynnik kierunkowy.
Jeśli proste mają być prostopadłe do podanej prostej to ich współczynniki kierunkowe muszą spełniać równanie ![]()
Oblicz współczynnik kierunkowy dla prostych prostopadłych do tej prostej:
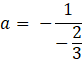
![]()
Prosta o równaniu 2x + 3y – 4 = 0.
Przekształć jej równanie na postać kierunkową:
![]()
![]()
![]()
Ta prosta jest równoległa do podanej prostej.
Prosta o równaniu 1,5x – y = 0.
Przekształć jej równanie na postać kierunkową:
![]()
![]()
![]()
Ta prosta jest prostopadła do podanej prostej.
Prosta o równaniu y = 1,5x + 2.
Przekształć jej współczynnik kierunkowy:
![]()
![]()
Ta prosta jest prostopadła do podanej prostej.
Prosta o równaniu -10y + 15x – 1 = 0.
Przekształć jej równanie na postać kierunkową:
![]()
![]()
![]()
![]()
Ta prosta jest prostopadła do podanej prostej.
Prosta o równaniu ![]()
Przekształć jej równanie na postać kierunkową:
![]()
![]()
Ta prosta nie jest prostopadła ani równoległa do podanej prostej.

Zauważ, że proste są prostopadłe, tylko wtedy, gdy ich współczynnik kierunkowy a spełnia podaną zależność ![]()
![]()
![]()

Ćwiczenie B.
217Ćwiczenie C.
218Zadanie 1.
220Zadanie 2.
220Zadanie 6.
220Zadanie 9.
221Zadanie 12.
221Zadanie 14.
221Zadanie 15.
221Zadanie 17.
221Zadanie 18.
222Zadanie 20.
222Zadanie 21.
222Ćwiczenie A.
223Ćwiczenie B.
224Przykład 2.
226Zadanie 1.
228Zadanie 2.
228Zadanie 4.
228Zadanie 5.
228Zadanie 7.
228Zadanie 8.
228Zadanie 9.
228Zadanie 11.
229Zadanie 12.
229Zadanie 14.
229Zadanie 15.
229Zadanie 16.
229Zadanie 1.
234Zadanie 3.
234Zadanie 4.
234Zadanie 6.
234Zadanie 7.
234Zadanie 8.
234Zadanie 9.
234Zadanie 13.
235Zadanie 15.
235Ćwiczenie B.
236Ćwiczenie C.
237Zadanie 1.
238Zadanie 3.
238Zadanie 4.
239Zadanie 5.
239Zadanie 6.
239Zadanie 8.
239Zadanie 9.
239Zadanie 10.
239Zadanie 11.
239Zadanie 12.
240Zadanie 13.
240Zadanie 1.
245Zadanie 2.
245Zadanie 5.
247Zadanie 6.
247Zadanie 7.
247Zadanie 8.
247Zadanie 11.
247Zadanie 12.
247Zadanie 15.
248Zadanie 16.
248Zadanie 17.
248Zadanie 18.
248Zadanie 1.
250Zadanie 7.
250Zadanie 8.
250
